如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点N,连接BM,DN.
(1)求证:四边形BMDN是菱形;
(2)若AB=4,AD=8,求MD的长
已知正方形纸片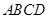 的边长为2.操作:如图1,将正方形纸片折叠,使顶点
的边长为2.操作:如图1,将正方形纸片折叠,使顶点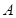 落在边
落在边 上的点
上的点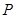 处(点
处(点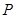 与
与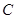 、
、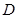 不重合),折痕为
不重合),折痕为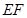 ,折叠后
,折叠后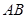 边落在
边落在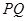 的位置,
的位置,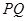 与
与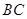 交于点
交于点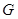 .
.
探究:观察操作结果,找到一个与
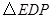 相似的三角形,并证明你的结论;
相似的三角形,并证明你的结论;当点
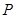 位于
位于 中点时,你找到的三角形与
中点时,你找到的三角形与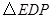 周长的比是多少(图2为备用图)?
周长的比是多少(图2为备用图)?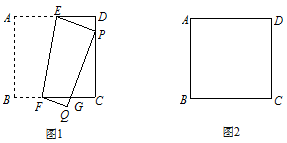
一次数学知识竞赛中,一共有25道题,答对一题得10分,答错(或不答)一题扣5分.设小明同学在这次竞赛中答对x道题.根据所给条件,完成下表:
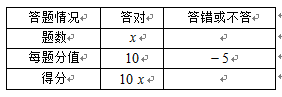
若小明同学的竞赛成绩超过100分,则他至少答对几道题?
如图,世博园段的浦江两岸互相平行,C、D是浦西江边间隔200m的两个场馆.海宝在浦东江边的宝钢大舞台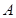 处,测得
处,测得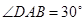 ,然后沿江边走了500m到达世博文化中心
,然后沿江边走了500m到达世博文化中心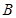 处,测得
处,测得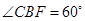 ,求世博园段黄浦江的宽度(结果可保留根号).
,求世博园段黄浦江的宽度(结果可保留根号).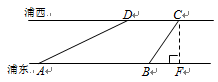
如图,已知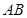 是⊙
是⊙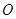 的直径,⊙
的直径,⊙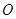 过
过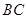 的中点
的中点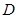 ,且
,且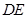 ⊥
⊥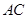 ,垂足为点
,垂足为点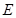 .
.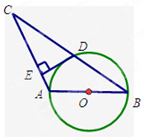
求证:
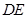 是⊙
是⊙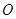 的切线;
的切线;若∠
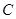 =
=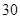 °,
°,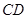 =10cm,求⊙
=10cm,求⊙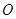 的半径.
的半径.
一只口袋中放着若干只红球和白球,这两种球除了颜色以外没有任何其他区别,袋中的球已经搅匀,蒙上眼睛从口袋中取出一只球,取出红球的概率是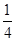 .
.取出白球的概率是多少?
如果袋中的白球有18只,那么袋中的红球有多少只?