解方程组(每小题4分,共8分)
(1)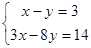
(2)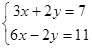
如图,在正方形ABCD中,E是AB边上任意一点,BG⊥CE,垂足为点O,交AC于点F,交AD于点G。
(1)证明:BE="AG" ;
(2)点E位于什么位置时,∠AEF=∠CEB,说明理由。
如图,在梯形ABCD中,AD∥BC,BC=2AD,点F、G分别是边BC、CD的中点,连接AF、FG,过点D作DE∥FG交AF于点E。
(1)求证:△AED≌△CGF;
(2)若梯形ABCD为直角梯形,∠B=90°,判断四边形DEFG是什么特殊四边形?并证明你的结论;
(3)若梯形ABCD的面积为a(平方单位),则四边形DEFG的面积为(平方单位)。(只写结果,不必说理)
某学校为了丰富大课间自由活动的内容,随机选取本校部分学生进行调查,调查内容是“你最喜欢的自由活动项目是什么?”,根据收集整理到的数据绘制成以下统计图

根据以上信息,解答下列问题:
(1)学校采用的调查方式是,被调查的样本 容量是。
容量是。
(2)请补充完整图中的条形统计图和扇形统计图(百分率精确到1%);
(3)假如你绘制图中扇形统计图,你认为踢毽子对应的扇形圆心角应为°(精确到1°).
(4)该校共有800名,请估计喜欢足球的学生人数。
某广告公司欲招聘广告策划人员一名,对A、B、C三名候选人进行了三项素质测试,他们的各项测试成绩如下表所示:(单位:分)
| 测试项目 |
测试成绩 |
||
| A |
B |
C |
|
| 创新 |
72 |
85 |
67 |
| 综合知识 |
50 |
74 |
70 |
| 语言 |
88 |
45 |
67 |
(1)如果根据三项测试的平均成绩来确定录用人选,那么谁将被录用?
(2)如果根据实际需要,公司将创新、综合知识、和语言三项测试成绩得分按4:3:1的比例来确定各人的测试成绩,此时 谁将被录用?
谁将被录用?