某广告公司欲招聘广告策划人员一名,对A、B、C三名候选人进行了三项素质测试,他们的各项测试成绩如下表所示:(单位:分)
| 测试项目 |
测试成绩 |
||
| A |
B |
C |
|
| 创 新 |
72 |
85 |
67 |
| 综合知识 |
50 |
74 |
70 |
| 语 言 |
88 |
45 |
67 |
(1)如果根据三项测试的平均成绩来确定录用人选,那么谁将被录用?
(2)如果根据实际需要,公司将创新、综合知识、和语言三项测试成绩得分按4:3:1的比例来确定各人的测试成绩,此时 谁将被录用?
谁将被录用?
问题背景
(1)如图1,
中,
分别交
,
于
,
两点,过点
作
交
于点
.请按图示数据填空:
四边形
的面积
△EFC的面积
△ADE的面积
探究发现
(2)在(1)中,若
,
,
与
间的距离为
.请证明
拓展迁移
(3)如图2,
的四个顶点在△ABC的三边上,若
、
、
的面积分别为2、5、3,试利用(2)中的结论求
的面积.

如图,在平面直角坐标系中,梯形ABCD的顶点坐标分别为A ,B
,B ,
, ,D
,D ,将梯形ABCD绕点D逆时针旋转90°得到梯形
,将梯形ABCD绕点D逆时针旋转90°得到梯形 .
.
(1)在平面直角坐标系中画出梯形A1B1C1D,则 的坐标为,
的坐标为, 的坐标为,
的坐标为, 的坐标为;
的坐标为;
(2)点C旋转到点 的路线长为(结果保留
的路线长为(结果保留 ).
).
如图,点B和点C分别为∠MAN两边上的点,AB=AC.
(1)按下列语句画出图形:
① AD⊥BC,垂足为D;
② ∠BCN的平分线CE与AD的延长线交于点E
③ 连结BE.
(2)在完成(1)后不添加线段和字母的情况下,请你写出除△ABD≌△ACD外的两对全等三角形:≌,≌;并选择其中的一对全等三角形予以证明.
计算:
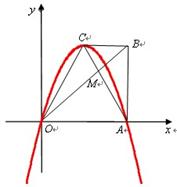
如图,在直角梯形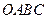 中,
中,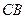 ∥
∥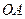 ,
,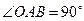 ,点
,点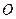 为坐标原点,点
为坐标原点,点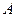 在
在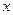 轴的正半轴上,对角线
轴的正半轴上,对角线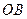 ,
,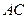 相交于点
相交于点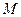 ,
,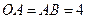 ,
,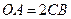 .
.
(1)线段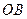 的长为,点
的长为,点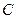 的坐标为;
的坐标为;
(2)求△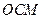 的面积;
的面积;
(3)求过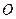 ,
,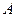 ,
,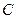 三点的抛物线的解析式;
三点的抛物线的解析式;
(4)若点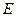 在(3)的抛物线的对称轴上,点
在(3)的抛物线的对称轴上,点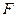 为该抛物线上的点,且以
为该抛物线上的点,且以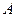 ,
,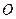 ,
,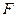 ,
,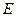 四点为顶点的四边形为平行四边形,求点
四点为顶点的四边形为平行四边形,求点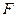 的坐标.
的坐标.