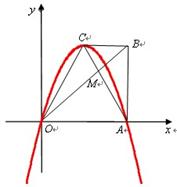
如图,在直角梯形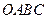 中,
中,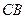 ∥
∥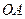 ,
,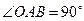 ,点
,点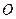 为坐标原点,点
为坐标原点,点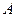 在
在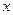 轴的正半轴上,对角线
轴的正半轴上,对角线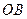 ,
,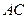 相交于点
相交于点 ,
,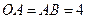 ,
,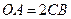 .
.
(1)线段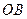 的长为 ,点
的长为 ,点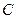 的坐标为 ;
的坐标为 ;
(2)求△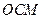 的面积;
的面积;
(3)求过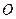 ,
,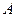 ,
,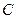 三点的抛物线的解析式;
三点的抛物线的解析式;
(4)若点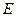 在(3)的抛物线的对称轴上,点
在(3)的抛物线的对称轴上,点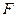 为该抛物线上的点,且以
为该抛物线上的点,且以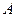 ,
,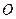 ,
,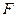 ,
,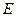 四点为顶点的四边形为平行四边形,求点
四点为顶点的四边形为平行四边形,求点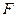 的坐标.
的坐标.
2022年的冬奥会在北京举行,其中冬奥会吉祥物“冰墩墩”深受人们喜爱,多地出现了“一墩难求”的场面.某纪念品商店在开始售卖当天提供 个“冰墩墩”后很快就被抢购一空,该店决定让当天未购买到的顾客可通过预约在第二天优先购买,并且从第二天起,每天比前一天多供应m个(m为正整数).经过连续15天的销售统计,得到第 天( ,且 为正整数)的供应量 (单位:个)和需求量 (单位:个)的部分数据如下表,其中需求量 与 满足某二次函数关系.(假设当天预约的顾客第二天都会购买,当天的需求量不包括前一天的预约数)
|
第 天 |
|
|
… |
|
… |
|
… |
|
|
供应量 (个) |
|
|
… |
|
… |
|
… |
|
|
需求量 (个) |
|
|
… |
|
… |
|
… |
|
(1)直接写出 与 和 与 的函数关系式;(不要求写出 的取值范围)
(2)已知从第 天开始,有需求的顾客都不需要预约就能购买到(即前 天的总需求量超过总供应量,前 天的总需求量不超过总供应量),求 的值;(参考数据:前 天的总需求量为 个)
(3)在第(2)问 取最小值的条件下,若每个“冰墩墩”售价为 元,求第 天与第 天的销售额.
如图,已知 为 上一点,点 在直径 的延长线上, 与 相切,交 的延长线于点 ,且 .
(1)判断 与 的位置关系,并说明理由;
(2)若 , ,
①求 的半径;
②求 的长.

为落实国家“双减”政策,立德中学在课后托管时间里开展了“音乐社团、体育社团、文学社团、美术社团”活动.该校从全校 名学生中随机抽取了部分学生进行“你最喜欢哪一种社团活动(每人必选且只选一种)”的问卷调查,根据调查结果,绘制了如图所示的两幅不完整的统计图.
根据图中信息,解答下列问题:
(1)参加问卷调查的学生共有____人;
(2)条形统计图中m的值为____,扇形统计图中 的度数为____;
(3)根据调查结果,可估计该校 名学生中最喜欢“音乐社团”的约有____人;
(4)现从“文学社团”里表现优秀的甲、乙、丙、丁四名同学中随机选取两名参加演讲比赛,请用列表或画树状图的方法求出恰好选中甲和乙两名同学的概率.

如图,在平行四边形 中,点 分别在边 上,且四边形 为正方形.
(1)求证: ;
(2)已知平行四边形 的面积为 , ,求 的长.

已知关于 的一元二次方程 有两个不等实数根 .
(1)求 的取值范围;
(2)若 ,求 的值.