已知等差数列 中,
中,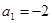 ,公差
,公差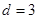 ;数列
;数列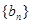 中,
中, 为其前n项和,满足:
为其前n项和,满足: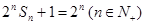
(Ⅰ)记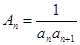 ,求数列
,求数列 的前
的前 项和
项和 ;
;
(Ⅱ)求证:数列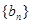 是等比数列;
是等比数列;
(Ⅲ)设数列 满足
满足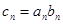 ,
, 为数列
为数列 的前
的前 项积,若数列
项积,若数列 满足
满足 ,且
,且 ,求数列
,求数列 的最大值.
的最大值.
如图,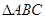 中,
中,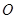 是
是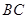 的中点,
的中点,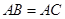 ,
,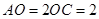 .将
.将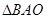 沿
沿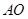 折起,使
折起,使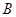 点与图中
点与图中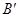 点重合.
点重合.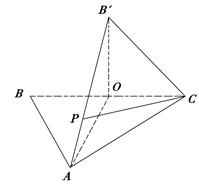
(Ⅰ)求证: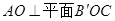 ;
;
(Ⅱ)当三棱锥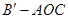 的体积取最大时,求二面角
的体积取最大时,求二面角 的余弦值;
的余弦值;
(Ⅲ)在(Ⅱ)的条件下,试问在线段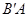 上是否存在一点
上是否存在一点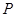 ,使
,使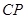 与平面
与平面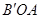 所成的角的正弦值为
所成的角的正弦值为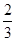 ?证明你的结论.
?证明你的结论.
已知函数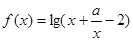 ,其中
,其中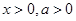
(Ⅰ)求函数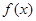 的定义域;
的定义域;
(Ⅱ)若对任意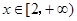 恒有
恒有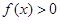 ,试确定
,试确定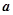 的取值范围.
的取值范围.
设函数
(Ⅰ)当 时,求
时,求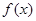 的值域;
的值域;
(Ⅱ)已知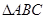 中,角
中,角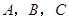 的对边分别为
的对边分别为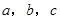 ,若
,若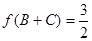 ,
,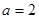 ,求
,求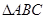 面积的最大值.
面积的最大值.
(本小题满分12分)已知函数 有如下性质:如果常数
有如下性质:如果常数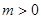 ,那么该函数在
,那么该函数在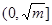 上是减函数,在
上是减函数,在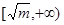 上是增函数。
上是增函数。
(Ⅰ)如果函数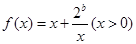 在
在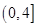 上是减函数,在
上是减函数,在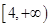 上是增函数,求实数
上是增函数,求实数 的值;
的值;
(Ⅱ)求函数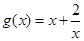 在
在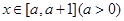 上的最小值;
上的最小值;
(Ⅲ)设常数 ,求函数
,求函数 的最大值.
的最大值.