(本小题满分10分)选修4-5:不等式选讲
(1)已知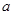 ,
,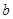 都是正数,且
都是正数,且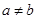 ,求证:
,求证: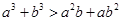 ;
;
(2)已知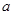 ,
,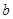 ,
,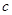 都是正数,求证:
都是正数,求证: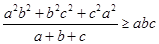 .
.
已知函数f(x)=log2 +log2(x﹣1)+log2(p﹣x).
+log2(x﹣1)+log2(p﹣x).
(1)求函数f(x)的定义域;
(2)求函数f(x)的值域.
已知函数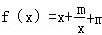 (x∈[1,+∞)且m<1).
(x∈[1,+∞)且m<1).
(Ⅰ)用定义证明函数f(x)在[1,+∞)上为增函数;
(Ⅱ)设函数 ,若[2,5]是g(x)的一个单调区间,且在该区间上g(x)>0恒成立,求实数m的取值范围.
,若[2,5]是g(x)的一个单调区间,且在该区间上g(x)>0恒成立,求实数m的取值范围.
某校高一年级甲、已两班准备联合举行晚会,两班各派一人先进行转盘游戏,胜者获得一件奖品,负者表演一个节目.甲班的文娱委员利用分别标有数字1,2,3,4,5,6,7的两个转盘(如图所示),设计了一种游戏方案:两人同时各转动一个转盘一次,将转到的数字相加,和为偶数时甲班代表获胜,否则乙班代表获胜.
(Ⅰ)根据这个游戏方案,转到的两数之和会出现哪些可能的情况?
(Ⅱ)游戏方案对双方是否公平?请说明理由.
已知函数f(x)=ax﹣1(a>0且a≠1)
(1)若函数y=f(x)的图象经过P(3,4)点,求a的值;
(2)比较 与f(﹣2.1)大小,并写出比较过程.
与f(﹣2.1)大小,并写出比较过程.
已知函数f(x)=
(Ⅰ)求f(1),f(﹣3),f(a+1)的值;
(Ⅱ)求函数f(x)的零点.