于定义在D上的函数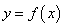 ,若同时满足
,若同时满足
①存在闭区间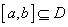 ,使得任取
,使得任取 ,都有
,都有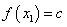 (
( 是常数);
是常数);
②对于D内任意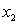 ,当
,当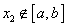 时总有
时总有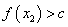 ;
;
则称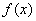 为“平底型”函数.
为“平底型”函数.
(1)判断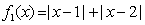 ,
,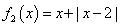 是否是“平底型”函数?简要说明理由;
是否是“平底型”函数?简要说明理由;
(2)设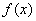 是(1)中的“平底型”函数,若
是(1)中的“平底型”函数,若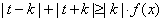 ,(
,(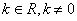 )
)
对一切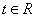 恒成立,求实数
恒成立,求实数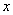 的范围;
的范围;
(3)若 是“平底型”函数,求
是“平底型”函数,求 和
和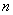 的值.
的值.
在直角坐标系 中,已知中心在原点,离心率为
中,已知中心在原点,离心率为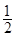 的椭圆E的一个焦点为圆
的椭圆E的一个焦点为圆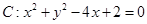 的圆心.
的圆心.
⑴求椭圆E的方程;
⑵设P是椭圆E上一点,过P作两条斜率之积为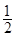 的直线
的直线 ,当直线
,当直线 都与圆
都与圆 相切时,求P点坐标.
相切时,求P点坐标.
某个公园有个池塘,其形状为直角△ABC,∠C=90°,AB=2百米,BC=1百米.
(1)现在准备养一批供游客观赏的鱼,分别在AB、BC、CA上取点D,E,F,如图(1),使得EF‖AB,EF⊥ED,在△DEF喂食,求△DEF面积S△DEF的最大值;
(2)现在准备新建造一个荷塘,分别在AB,BC,CA上取点D,E,F,如图(2),建造△DEF连廊(不考虑宽度)供游客休憩,且使△DEF为正三角形,求△DEF边长的最小值.
如图长方体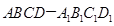 中,底面
中,底面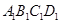 是正方形,
是正方形,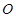 是
是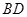 的中点,
的中点,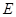 是棱
是棱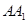 上任意一点.
上任意一点.
⑴求证: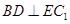 ;
;
⑵如果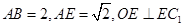 ,求
,求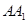 的长.
的长.
设向量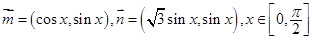 .
.
⑴若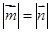 ,求
,求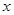 的值;
的值;
⑵设函数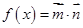 ,求
,求 的最大值.
的最大值.
已知函数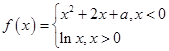 ,其中
,其中 是实数,设
是实数,设 为该函数的图象上的两点,且
为该函数的图象上的两点,且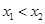 .
.
⑴指出函数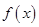 的单调区间;
的单调区间;
⑵若函数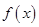 的图象在点
的图象在点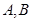 处的切线互相垂直,且
处的切线互相垂直,且 ,求
,求 的最小值;
的最小值;
⑶若函数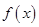 的图象在点
的图象在点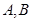 处的切线重合,求
处的切线重合,求 的取值范围.
的取值范围.