某个公园有个池塘,其形状为直角△ABC,∠C=90°,AB=2百米,BC=1百米.
(1)现在准备养一批供游客观赏的鱼,分别在AB、BC、CA上取点D,E,F,如图(1),使得EF‖AB,EF⊥ED,在△DEF喂食,求△DEF 面积S△DEF的最大值;
(2)现在准备新建造一个荷塘,分别在AB,BC,CA上取点D,E,F,如图(2),建造△DEF连廊(不考虑宽度)供游客休憩,且使△DEF为正三角形,求△DEF边长的最小值.
如图四棱锥E—ABCD中,底面ABCD是平行四边形。∠ABC=45°,BE=BC=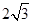 EA=EC=6,M为EC中点,平面BCE⊥平面ACE,AE⊥EB
EA=EC=6,M为EC中点,平面BCE⊥平面ACE,AE⊥EB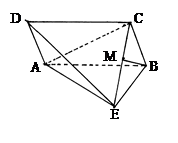
(I)求证:AE⊥BC(II)求四棱锥E—ABCD体积
某糖厂为了了解一条自动生产线上袋装白糖的重量,随机抽取了100袋,并称出每袋白糖的重量(单位:g),得到如下频率分布表。
| 分组 |
频数 |
频率 |
| [485.5,490.5) |
10 |
 |
| [490.5,495.5) |
 |
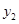 |
| [495.5,500.5) |
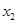 |
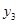 |
| [500.5,505.5] |
10 |
|
| 合计 |
100 |
表中数据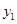 ,
,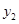 ,
,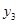 成等差数列。
成等差数列。
(I)将有关数据分别填入所给的频率。分布表的所有空格内,并画出频率分布直方图。
(II)在这100包白糖的重量中,估计其中位数。
在△ABC中,角A为锐角,记角A、B、C所对的边分别为a、b、c,设向量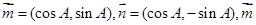 与
与 的夹角为
的夹角为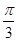 。
。
(I)求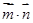 及角A的大小。
及角A的大小。
(II)若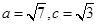 ,求△ABC的面积。
,求△ABC的面积。
已知函数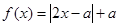 。
。
(1)若不等式 的解集为
的解集为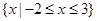 ,求实数
,求实数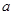 的值;
的值;
(2)在(1)的条件下,若存在实数n使 成立,求实数m的取值范围。
成立,求实数m的取值范围。
在平面直角坐标系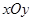 中,直线
中,直线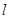 的参数方程为
的参数方程为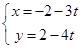 (t为参数),它与曲线
(t为参数),它与曲线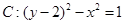 交于A、B两点。
交于A、B两点。
(1)求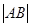 的长;
的长;
(2)在以 为极点,
为极点, 轴的正半轴为极轴建立极坐标系,设点P的极坐标为
轴的正半轴为极轴建立极坐标系,设点P的极坐标为 ,求点P到线段AB中点M的距离。
,求点P到线段AB中点M的距离。