某糖厂为了了解一条自动生产线上袋装白糖的重量,随机抽取了100袋,并称出每袋白糖的重量(单位:g),得到如下频率分布表。
| 分组 |
频数 |
频率 |
| [485.5,490.5) |
10 |
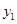 |
| [490.5,495.5) |
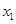 |
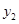 |
| [495.5,500.5) |
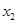 |
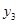 |
| [500.5,505.5] |
10 |
|
| 合计 |
100 |
|
表中数据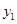 ,
,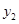 ,
,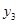 成等差数列。
成等差数列。
(I)将有关数据分别填入所给的频率。分布表的所有空格内,并画出频率分布直方图。
(II)在这100包白糖的重量中,估计其中位数。
已知二次函数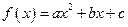 满足条件:①
满足条件:① 是
是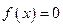 的两个零点;②
的两个零点;②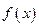 的最小值为
的最小值为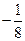
(1)求函数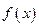 的解析式;
的解析式;
(2)设数列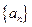 的前
的前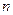 项积为
项积为 ,且
,且 ,
,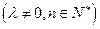 ,求数列
,求数列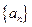 的前
的前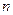 项和
项和
(3)在(2)的条件下,当 时,若
时,若 是
是 与
与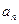 的等差中项,试问数列
的等差中项,试问数列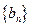 中
中
第几项的值最小?并求出这个最小值。
已知函数 。
。
(I)若从集合{0,1,2,3}中任取一个元素作为 ,从集合{0,1,2}中任取一个元素作为b,求方程
,从集合{0,1,2}中任取一个元素作为b,求方程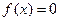 有两个不等实数根的概率;
有两个不等实数根的概率;
(II)若从区间[0,2]中任取一个数作为 ,从区间
,从区间 中任取一个数作为
中任取一个数作为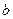 ,求方程
,求方程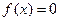 没有实数根的概率。
没有实数根的概率。
已知抛物线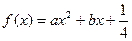 与直线
与直线 相切于点A(1,1)。
相切于点A(1,1)。
(1)求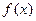 的解析式;
的解析式;
(2)若对任意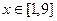 ,不等式
,不等式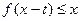 恒成立,求实数
恒成立,求实数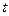 的取值范围。
的取值范围。
已知四棱锥P-ABCD 的直观图与三视图如图所示
的直观图与三视图如图所示
(1)求四棱锥P-ABCD的体 积;
积;
(2)若E为侧棱PC的中点,求证:PA//平面BDE.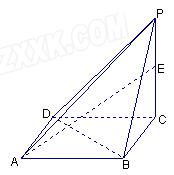

已知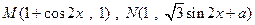
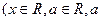 是常数),且
是常数),且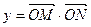 (
( 为坐标原点).
为坐标原点).
(1)求函数 的单调递增区间;
的单调递增区间;
(2)若 时,
时, 的最大值为4,求
的最大值为4,求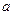 的值;
的值;