已知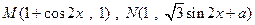
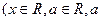 是常数),且
是常数),且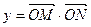 (
( 为坐标原点).
为坐标原点).
(1)求函数 的单调递增区间;
的单调递增区间;
(2)若 时,
时, 的最大值为4,求
的最大值为4,求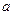 的值;
的值;
(本小题满分12分) 设a1,d为实数,首项为a1,公差为d的等差数列{an}的前n项和为Sn,满足S5S6+15=0,S5="5" ;
(1)求通项an及Sn;
(2)设 是首项为1,公比为3的等比数列.求数列{bn}的通项公式及其前n项和Tn。
是首项为1,公比为3的等比数列.求数列{bn}的通项公式及其前n项和Tn。
(本小题满分14分)已知数列{an}满足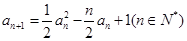 且a1=3。
且a1=3。
(1)求a2,a3,a4的值及数列{an}的通项an;
(2)设数列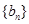 满足
满足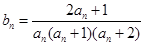 ,Sn为数列
,Sn为数列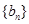 的前n项和,求证:
的前n项和,求证: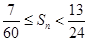 。
。
(本小题满分13分)已知函数 为自然对数的底数)
为自然对数的底数)
(1)求函数 的最小值;
的最小值;
(2)若 ≥0对任意的x∈R恒成立,求实数a的值;
≥0对任意的x∈R恒成立,求实数a的值;
(3)在(2)的条件下,证明:
(本小题满分12分)合肥一中生活区内建有一块矩形休闲区域ABCD,AB=100米,BC=50 米,为了便于同学们平时休闲散步,学校后勤部门将在这块区域内铺设三条小路OE、EF和OF,考虑到学校整体规划,要求O是AB的中点,点E在边BC上,点F在边AD上,且OE⊥OF,如图所示.
米,为了便于同学们平时休闲散步,学校后勤部门将在这块区域内铺设三条小路OE、EF和OF,考虑到学校整体规划,要求O是AB的中点,点E在边BC上,点F在边AD上,且OE⊥OF,如图所示.
(1)设∠BOE= ,试将△OEF的周长
,试将△OEF的周长 表示成
表示成 的函数关系式,并求出此函数的定义域;
的函数关系式,并求出此函数的定义域;
(2)经核算,三条路每米铺设费用均为800元,试问如何设计才能使铺路的总费用最低?并求出最低总费用.
(本小题满分12分)利用已学知识证明:
(1) 。
。
(2)已知△ABC的外接圆的半径为2,内角A,B,C满足 ,求△ABC的面积。
,求△ABC的面积。