如图,在边长为1的正六边形ABCDEF中,其中心为点O.
(1)在正六边形ABCDEF的边上任取一点P,求满足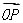 在
在 上的投影大于
上的投影大于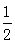 的概率;
的概率;
(2)从A,B,C,D,E,F这六个点中随机选取两个点,记这两个点之间的距离为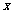 ,求
,求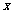 大于等于
大于等于 的概率.
的概率.
(本小题满分12分)
已知数列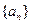 满足:
满足: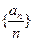 是公差为1的等差数列,且
是公差为1的等差数列,且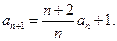
(1)求数列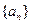 的通项公式
的通项公式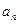 ;
;
(2)设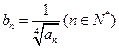 ,求证:
,求证: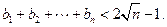
(本小题满分12分)
已知点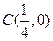 ,椭圆
,椭圆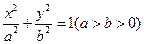 的右准线
的右准线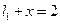 与x轴相交于点D,右焦点F到上顶点的距离为
与x轴相交于点D,右焦点F到上顶点的距离为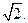
(1)求椭圆的方程;
(2)是否存在过点F且与x轴不垂直的直线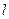 与椭圆交于A、B两点,使得
与椭圆交于A、B两点,使得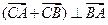 ?若存在,求出直线
?若存在,求出直线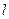 ;若不存在,说明理由。
;若不存在,说明理由。
(本小题满分12分)
函数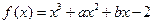 的图象在与y轴交点的切线方程为
的图象在与y轴交点的切线方程为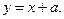
(1)求函数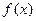 的解析式;
的解析式;
(2)设函数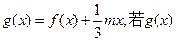 存在极值,求实数m的取值范围。
存在极值,求实数m的取值范围。
本小题满分13分)
如图,已知ABCD是边长为2的正方形,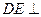 平面ABCD,
平面ABCD, 平面ABCD,且FB=2DE=2。
平面ABCD,且FB=2DE=2。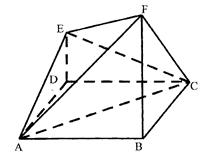
(1)求点E到平面FBC的距离;
(2)求证:平面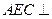 平面AFC。
平面AFC。
(本小题满分13分)
某射手A第n次射击时击中靶心的概率为
(1)求A射击5次,直到第5次才击中靶心的概率P;
(2)若A共射击3次,求恰好击中1次靶心的概率。