(本小题满分12分)某旅行社为调查市民喜欢“人文景观”景点是否与年龄有关,随机抽取了55名市民,得到数据如下表:
| |
喜欢 |
不喜欢 |
合计 |
| 大于40岁 |
20 |
5 |
25 |
| 20岁至40岁 |
10 |
20 |
30 |
| 合计 |
30 |
25 |
55 |
(1)判断是否有99.5%的把握认为喜欢“人文景观”景点与年龄有关?
(2)用分层抽样的方法从喜欢“人文景观”景点的市民中随机抽取6人作进一步调查,将这6位市民作为一个样本,从中任选2人,求恰有1位“大于40岁”的市民和1位“20岁至40岁”的市民的概率.
下面的临界值表供参考:
 |
0.15 |
0.10 |
0.05 |
0.025 |
0.010 |
0.005 |
0.001 |
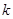 |
2.072 |
2.706 |
3.841 |
5.024 |
6.635 |
7.879 |
10.828 |
(参考公式: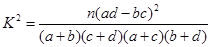 ,其中
,其中 )
)
已知椭圆 :
: 的左、右焦点分别为
的左、右焦点分别为 ,它的一条准线为
,它的一条准线为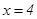 ,过点
,过点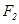 的直线与椭圆
的直线与椭圆 交于
交于 、
、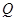 两点.当
两点.当 与
与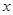 轴垂直时,
轴垂直时, .
.
(1)求椭圆 的方程;
的方程;
(2)若 ,求
,求 的内切圆面积最大时正实数
的内切圆面积最大时正实数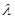 的值.
的值.
已知 是公比大于
是公比大于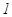 的等比数列,它的前
的等比数列,它的前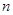 项和为
项和为 , 若
, 若 ,
,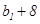 ,
,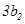 ,
,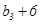 成等差数列,且
成等差数列,且 ,
,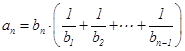 (
(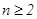 ).
).
(1)求 ;
;
(2)证明: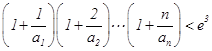 (其中
(其中 为自然对数的底数).
为自然对数的底数).
如图,已知直三棱柱 中,
中,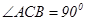 ,
,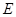 是棱
是棱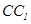 上的动点,
上的动点,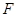 是
是 的中点,
的中点, ,
,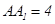 .
.
(1)当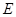 是棱
是棱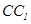 的中点时,求证:
的中点时,求证: 平面
平面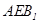 ;
;
(2)在棱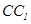 上是否存在点
上是否存在点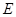 ,使得二面角
,使得二面角 的大小是
的大小是 ?若存在,求出
?若存在,求出 的长,若不存在,请说明理由.
的长,若不存在,请说明理由.
某大学对该校参加某项活动的志愿者实施“社会教育实施”学分考核,该大学考核只有合格和优秀两个等次.若某志愿者考核为合格,授予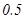 个学分;考核为优秀,授予
个学分;考核为优秀,授予 个学分.假设该校志愿者甲、乙考核为优秀的概率分别为
个学分.假设该校志愿者甲、乙考核为优秀的概率分别为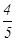 、
、 ,乙考核合格且丙考核优秀的概率为
,乙考核合格且丙考核优秀的概率为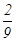 .甲、乙、丙三人考核所得等次相互独立.
.甲、乙、丙三人考核所得等次相互独立.
(1)求在这次考核中,志愿者甲、乙、丙三人中至少有一名考核为优秀的概率;
(2)记在这次考核中,甲、乙、丙三名志愿者所得学分之和为随机变量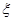 ,求随机变量
,求随机变量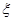 的
的
分布列和数学期望.
在锐角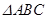 中,角
中,角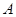 、
、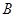 、
、 所对的边分别为
所对的边分别为 、
、 、
、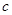 .
.
且 .
.
(1)求角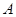 的大小及角
的大小及角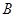 的取值范围;
的取值范围;
(2)若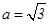 ,求
,求 的取值范围.
的取值范围.