已知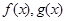 都是定义在
都是定义在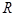 上的函数,
上的函数, ,
,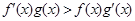 ,且
,且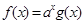
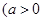 ,且
,且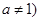 ,
,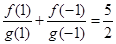 .若数列
.若数列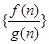 的前
的前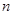 项和大于
项和大于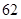 ,则
,则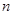 的最小值为()
的最小值为()
| A.6 | B.7 | C.8 | D.9 |
如图,用一边长为 的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,将表面积为
的正方形硬纸,按各边中点垂直折起四个小三角形,做成一个蛋巢,将表面积为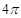 的鸡蛋(视为球体)放入其中,蛋巢形状保持不变,则鸡蛋中心(球心)与蛋巢底面的距离为()
的鸡蛋(视为球体)放入其中,蛋巢形状保持不变,则鸡蛋中心(球心)与蛋巢底面的距离为()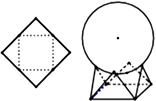
A.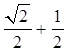 |
B.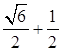 |
C.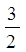 |
D.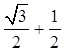 |
已知函数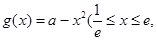
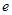 为自然对数的底数)与
为自然对数的底数)与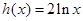 的图象上存在关于
的图象上存在关于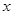 轴对称的点,则实数
轴对称的点,则实数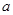 的取值范围是()
的取值范围是()
A.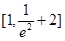 |
B.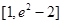 |
C.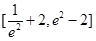 |
D.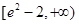 |
图一是某校学生身高的条形统计图,从左到右表示学生人数依次记为A1、A2、…、A10(如A2表示身高在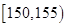 内的人数)。图二是统计图一中身高在一定范围内学生人数的一个算法流程图。现要统计身高在
内的人数)。图二是统计图一中身高在一定范围内学生人数的一个算法流程图。现要统计身高在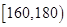 内的学生人数,那么在流程图中的判断框内应填写的条件及输出的
内的学生人数,那么在流程图中的判断框内应填写的条件及输出的 值分别是()
值分别是()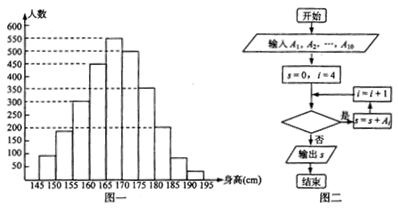
A. |
B.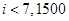 |
C. |
D.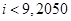 |
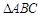 中,“角
中,“角 成等差数列”是“
成等差数列”是“ ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |