(本小题满分12分)某校在一次对是否喜欢英语学科的学生的抽样调查中,随机抽取了100名同学,相关的数据如下表所示:
| |
不喜欢英语 |
喜欢英语 |
总计 |
| 男生 |
40 |
18 |
58 |
| 女生 |
15 |
27 |
42 |
| 总计 |
55 |
45 |
100 |
(Ⅰ)试运用独立性检验的思想方法分析:是否有99 %的把握认为“学生是否喜欢英语与性别有关?”说明理由.
(Ⅱ)用分层抽样方法在喜欢英语学科的学生中随机抽取5名,女学生应该抽取几名?
(Ⅲ)在上述抽取的5名学生中任取2名,求恰有1名学生为男性的概率.
附: =
= ,
,
 |
0.100 |
0.050 |
0.025 |
0.01 |
0.001 |
 |
2.706 |
3.841 |
5.024 |
6.635 |
10.828 |
画出计算 的程序框图,并写出相应的程序.
的程序框图,并写出相应的程序.
已知三角形ABC的顶点坐标为A(-1,5)、B(-2,-1)、C(4,3),M是BC边上的中点.
(1)求AB边所在的直线方程;
(2)求中线AM的长
(3)求AB边的高所在直线方程.
已知动点M到点A(2,0)的距离是它到点B(8,0)的距离的一半,
求:(1)动点M的轨迹方程;
(2)若N为线段AM的中点,试求点N的轨迹.
(本小题满分14分)
已知函数 的单调递增区间为
的单调递增区间为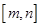 ,
,
(Ⅰ)求证: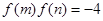 ;
;
(Ⅱ)当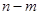 取最小值时,点
取最小值时,点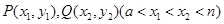 是函数
是函数 图象上的两点,若存在
图象上的两点,若存在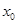 使得
使得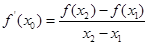 ,求证:
,求证:
(本小题满分14分)
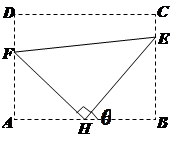
如图:某污水处理厂要在一个矩形污水处理池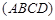 的池底水平铺设污水净化管道
的池底水平铺设污水净化管道 ,
,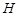 是直角顶点)来处理污水,管道越短,铺设管道的成本越低.设计要求管道的接口
是直角顶点)来处理污水,管道越短,铺设管道的成本越低.设计要求管道的接口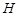 是
是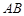 的中点,
的中点, 分别落在线段
分别落在线段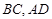 上。已知
上。已知 米,
米, 米,记
米,记 。
。
(Ⅰ)试将污水净化管道的长度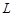 表示为
表示为 的函数,并写出定义域;
的函数,并写出定义域;
(Ⅱ)若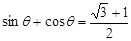 ,求此时管道的长度
,求此时管道的长度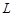 ;
;
(Ⅲ)问:当 取何值时,铺设管道的成本最低?并求出此时管道的长度。
取何值时,铺设管道的成本最低?并求出此时管道的长度。