如图所示，建筑工人正在使用打夯机将桩料打入泥土中以加固地基。打夯前，先将桩料扶起，使其缓慢直立进入泥土中，每次卷扬机都通过滑轮用轻质钢丝绳将夯锤提升到距离桩顶h0=5m处再释放，让夯锤自由下落，夯锤砸在桩料上并不弹起，而随桩料一起向下运动。设夯锤和桩料的质量均为m=500 kg，泥土对桩料的阻力为f=kh，其中常数k=2.0×104N/m，h是桩料深入泥土的深度。卷扬机使用电动机来驱动，卷扬机和电动机总的工作效率为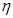
=95%，每次卷扬机需用20 s的时间提升夯锤。提升夯锤时忽略加速和减速的过程，不计夯锤提升时的动能，也不计滑轮的摩擦。夯锤和桩料的作用时间极短，g取10
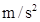，求：
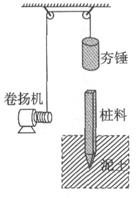
（1）在提升夯锤的过程中，电动机的输入功率；（结果保留2位有效数字）
（2）打完第一夯后，桩料进入泥土的深度。
两物块A、B用轻弹簧相连，质量均为2 kg，初始时弹簧处于原长，A．B两物块都以v＝6 m／s的速度在光滑的水平地面上运动，质量1 kg的物块C静止在前方，如图所示。B与C发生弹性碰撞。求在以后的运动中：
（1）物块C的速度为多大?
（2）弹簧的弹性势能的最大值是多少?
如图为用某种透明材料制成的一块柱体形棱镜的水平截面图,FD为
圆周,圆心为O.某单色光线a从AB面入射,入射角θ1=60°,它射入棱镜后射在BF面上的O点并恰好不从BF面射出.求
①该棱镜对单色光线a的折射率n？
②改用波长λ更长的单色光线b从AB面入射，入射角
同样为θ1=60°时,判断单色光线b能从BF面射出吗？说出理由.
如图所示，在x轴上方有垂直于x0y平面向里的匀强磁场，磁感应强度为B。在x轴下方有沿y轴负方向的匀强电场，场强为E，一质量为m，电荷量为-q的粒子从坐标原点沿着y轴正方向射出，射出之后，第三次到达x轴时，它与点O的距离为L，不计粒子所受重力。求：
（1）此粒子射出的速度v；
（2）运动的总路程X。
如图两根正对的平行金属直轨道MN、M´N´位于同一水平面上,两轨道间距L=0.50m.轨道的MM′端之间接一阻值R=0.40Ω的定值电阻,NN′端与两条位于竖直面内的半圆形光滑金属轨道NP、N′P′平滑连接,两半圆轨道的半径均为 R0 =0.50m.直轨道的右端处于竖直向下、磁感应强度B =0.64T的匀强磁场中,磁场区域的宽度d=0.80m,且其右边界与NN′重合.现有一质量 m =0.20kg、电阻 r =0.10Ω的导体杆ab静止在距磁场的左边界s=2.0m处.在与杆垂直的水平恒力 F =2.0N的作用下ab杆开始运动,当运动至磁场的左边界时撤去F,结果导体ab恰好能以最小速度通过半圆形轨道的最高点PP′.已知导体杆ab在运动过程中与轨道接触良好,且始终与轨道垂直,导体杆ab与直轨道间的动摩擦因数 μ=0.10,轨道的电阻可忽略不计,取g=10m/s2，求：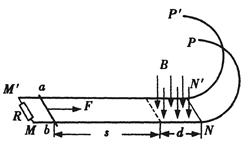
①导体杆穿过磁场的过程中通过电阻R上的电荷量
②导体杆穿过磁场的过程中整个电路产生的焦耳热
截面积为0.2m2的100匝电阻可以忽略不计的线圈A，处在均匀磁场中，磁场的方向垂直线圈截面，如图所示，磁感应强度为B =（0.6－0.2t）T（t为时间，以秒为单位），R1=4Ω，R2=6Ω，C=3
F，线圈电阻不计，求：
（1）闭合S2后，通过R2的电流大小和方向；
（2）S1切断后，通过R2的电量。