（本题12分）某工厂有甲种原料69千克，乙种原料52千克，现计划用这两种原料生产A，B两种型号的产品共80件，已知每件A型号产品需要甲种原料0．6千克，乙种原料0．9千克；每件B型号产品需要甲种原料1．1千克，乙种原料0．4千克．请解答下列问题：
（1）该工厂有哪几种生产方案？
（2）在这批产品全部售出的条件下，若1件A型号产品获利35元，1件B型号产品获利25元，（1）中哪种方案获利最大？最大利润是多少？
（3）在（2）的条件下，工厂决定将所有利润的25%全部用于再次购进甲、乙两种原料，要求每种原料至少购进4千克，且购进每种原料的数量均为整数．若甲种原料每千克40元，乙种原料每千克60元，请直接写出购买甲、乙两种原料之和最多的方案．
教材中第25章锐角的三角比，在这章的小结中有如下一段话：锐角三角比定量地描述了在直角三角形中边角之间的联系.在直角三角形中，一个锐角的大小与两条边长的比值相互唯一确定，因此边长与角的大小之间可以相互转化.
类似的，可以在等腰三角形中建立边角之间的联系，我们定义：等腰三角形中底边与腰的比叫做顶角的正对（sad）.如图，在△ABC中，AB=AC，顶角A的正对记作sadA，这时
sad A=
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
根据上述对角的正对定义，解下列问题：
（1）sad 
的值为（▼）
A． |
B．1 | C． |
D．2 |
（2）对于
，∠A的正对值sad A的取值范围是▼ .
（3）已知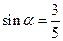
，其中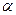
为锐角，试求sad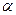的值.
如图，在△ABC中，∠ACB=
，D是AB延长线上一点，且BD=BC，CE⊥CD交AB于E.
（1）求证：△ACE∽△ADC；
（2）若BE∶EA=3∶2，求sin∠A的值.
如图，梯形ABCD中，AB‖CD，且AB∶CD=4∶3，E是CD的中点，AC与BE交于点F. 
（1）求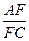
的值；
（2）若
，请用
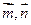来表示
已知二次函数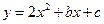
的图像经过点
与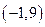
.
（1）求此函数的解析式；
（2）用配方法求此函数图像的顶点坐标.
如图，在△ABC中，BC=9，AB
,∠ABC=
. 
(1)求△ABC的面积；
(2)求cos∠C的值.