教材中第25章锐角的三角比,在这章的小结中有如下一段话:锐角三角比定量地描述了在直角三角形中边角之间的联系.在直角三角形中,一个锐角的大小与两条边长的比值相互唯一确定,因此边长与角的大小之间可以相互转化.
类似的,可以在等腰三角形中建立边角之间的联系,我们定义:等腰三角形中底边与腰的比叫做顶角的正对(sad).如图,在△ABC中,AB=AC,顶角A的正对记作sadA,这时
sad A= .容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
.容易知道一个角的大小与这个角的正对值也是相互唯一确定的.
根据上述对角的正对定义,解下列问题:
(1)sad  的值为( ▼ )
的值为( ▼ )
A. |
B.1 | C. |
D.2 |
(2)对于 ,∠A的正对值sad A的取值范围是 ▼ .
,∠A的正对值sad A的取值范围是 ▼ .
(3)已知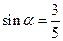 ,其中
,其中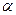 为锐角,试求sad
为锐角,试求sad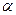 的值.
的值.
为了加强公民的节水意识,合理利用水资源,某市采用价格调控的手段达到节水的目的,该市自来水收费的收费标准如下表: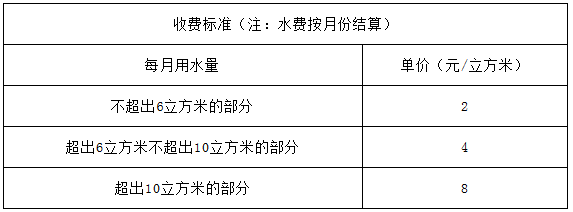
例如:某户居民1月份用水8立方米,应收水费为2×6+4×(8-6)=20(元).
请根据上表的内容解答下列问题:
(1)若某户居民2月份用水5立方米,则应收水费多少元?
(2)若某户居民3月份交水费36元,则用水量为多少立方米?
(3)若某户居民4月份用水a立方米(其中6<a<10),请用含a的代数式表示应收水费.
(4)若某户居民5、6两个月共用水18立方米(6月份用水量超过了10立方米),设5月份用水x立方米,请用含x的代数式表示该户居民5、6两个月共交水费多少元.
如图,四边形ABCD和ECGF都是正方形.
(1)写出表示阴影部分面积的代数式;(结果要求化简)
(2)当a=4时,求阴影部分的面积.
(1)已知|m|=3,|n|=2,且m<n,求m2+mn+n2的值.
(2)已知实数a、b在数轴上的位置如图,试化简|a|-|a+b|-2|a-b|.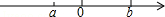
已知A=x2+x,B=x2-3x.
(1)计算:A-B和A+B.
(2)先化简,再求值:3(A-2B)-2( -2B),其中x=-
-2B),其中x=- .
.
把下列各实数填在相应的大括号内 ,-|-3|,
,-|-3|, ,0,
,0,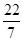 ,-3.
,-3.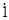 ,
,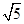 ,1-
,1- , 1.1010010001…(两个1之间依次多1个0)
, 1.1010010001…(两个1之间依次多1个0)
整数{ …};
分数{ …};
无理数{ …};