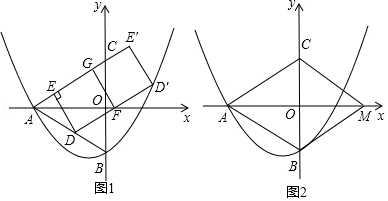
如图1,抛物线 经过 , 、 两点,点 在 轴上, 为等边三角形,点 从点 出发,沿 方向以每秒2个单位长度的速度向终点 运动,设运动时间为 秒 ,过点 作 于点 ,以 为边作矩形 ,使点 在 轴上,点 在 或 的延长线上.
(1)求抛物线的解析式;
(2)将矩形 沿 所在直线翻折,得矩形 ,当点 的对称点 落在抛物线上时,求此时点 的坐标;
(3)如图2,在 轴上有一点 , ,连接 、 ,在点 的运动过程中,设矩形 与四边形 重叠部分的面积为 ,直接写出 与 之间的函数关系式,并写出自变量 的取值范围.
如图,一次函数 的图象与反比例函数 的图象交于 , 两点,过 点作 轴的垂线,垂足为 , 面积为1.
(1)求反比例函数的解析式;
(2)在 轴上求一点 ,使 的值最小,并求出其最小值和 点坐标.

有大小两种货车,3辆大货车与4辆小货车一次可以运货18吨,2辆大货车与6辆小货车一次可以运货17吨.
(1)请问1辆大货车和1辆小货车一次可以分别运货多少吨?
(2)目前有33吨货物需要运输,货运公司拟安排大小货车共计10辆,全部货物一次运完.其中每辆大货车一次运货花费130元,每辆小货车一次运货花费100元,请问货运公司应如何安排车辆最节省费用?
绵阳某公司销售部统计了每个销售员在某月的销售额, 绘制了如下折线统计图和扇形统计图:

设销售员的月销售额为 (单 位: 万元) . 销售部规定: 当 时为“不称职”, 当 时为“基本称职”, 当 时为“称职”, 当 时为“优秀” . 根据以上信息, 解答下列问题:
(1) 补全折线统计图和扇形统计图;
(2) 求所有“称职”和“优秀”的销售员月销售额的中位数和众数;
(3) 为了调动销售员的积极性, 销售部决定制定一个月销售额奖励标准, 凡月销售额达到或超过这个标准的销售员将获得奖励 . 如果要使得所有“称职”和“优秀”的销售员的一半人员能获奖, 月销售额奖励标准应定为多少万元 (结 果取整数) ?并简述其理由 .
如图①,已知抛物线 的图象经过点 、 ,其对称轴为直线 ,过点 作 轴交抛物线于点 , 的平分线交线段 于点 ,点 是抛物线上的一个动点,设其横坐标为 .
(1)求抛物线的解析式;
(2)若动点 在直线 下方的抛物线上,连接 、 ,当 为何值时,四边形 面积最大,并求出其最大值;
(3)如图②, 是抛物线的对称轴 上的一点,在抛物线上是否存在点 使 成为以点 为直角顶点的等腰直角三角形?若存在,直接写出所有符合条件的点 的坐标;若不存在,请说明理由.

如图①,在四边形 中, 于点 , ,点 为 中点, 为线段 上的点,且 .
(1)求证: 平分 ;
(2)若 ,连接 ,当四边形 为平行四边形时,求线段 的长;
(3)如图②,若点 为 的中点,连接 、 ,求证: .
