如图①,在四边形 中, 于点 , ,点 为 中点, 为线段 上的点,且 .
(1)求证: 平分 ;
(2)若 ,连接 ,当四边形 为平行四边形时,求线段 的长;
(3)如图②,若点 为 的中点,连接 、 ,求证: .

在平面直角坐标系中,抛物线 与
与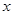 轴交于A、B两点(点A在点B的左侧),与
轴交于A、B两点(点A在点B的左侧),与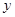 轴交于点C,点B的坐标为(3,0),将直线
轴交于点C,点B的坐标为(3,0),将直线 沿
沿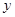 轴向上平移3个单位长度后恰好经过B、C两点。
轴向上平移3个单位长度后恰好经过B、C两点。
(1)求直线BC及抛物线的解析式;
(2)设抛物线的顶点为D,点P在抛物线的对称轴上,且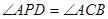 ,求点P的坐标.
,求点P的坐标.
(3)连结CD,求∠OCA与∠OCD两角和的度数.
在平面直角坐标系中,等边三角形OAB的边长是2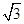 ,且OB边落在x轴的正半轴上,点A落在第一象限.将△OAB沿直线y=kx+b折叠,使点A落在x轴上,设点C是点A落在x轴上的对应点.
,且OB边落在x轴的正半轴上,点A落在第一象限.将△OAB沿直线y=kx+b折叠,使点A落在x轴上,设点C是点A落在x轴上的对应点.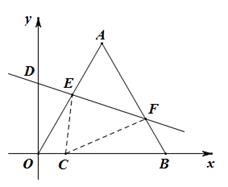
(1)如果点A恰好落在点C(0,0),求b的值;
(2)设点C的横坐标为m,求b与m之间的函数关系式;
(3)直接写出当b= 时,点C的坐标。
时,点C的坐标。
如图①②,图①是一个小朋友玩“滚铁环”的游戏,铁环是圆形的,铁环向前滚动时,铁环钩保持与铁环相切.将这个游戏抽象为数学问题,如图②.已知铁环的半径为5个单位(每个单位为5cm),设铁环中心为O,铁环钩与铁环相切点为M,铁环与地面接触点为A,∠MOA=α,且sinα=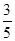 .
.
(1)求点M离地面AC的高度BM(单位:厘米);
(2)设人站立点C与点A的水平距离AC等于11个单位,求铁环钩MF的长度(单位:厘米).
如图,在△ABC中,AB=AC,D是BC上的任意一点.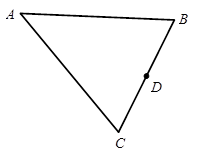
(1)过A、B、D三点作⊙O,交线段AC于点E(用直尺和圆规作图,保留作图痕迹,不写作法);
(2)若 =
=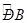 ,求证:AB是⊙O的直径;
,求证:AB是⊙O的直径;
(3)在(2)的条件下,若AB=5,BC=6,求AE的长
某市某幼儿园六一期间举行亲子游戏,主持人请三位家长分别带自己的孩子参加游戏,主持人准备把家长和孩子重新组合完成游戏,A、B、C分别表示三位家长,他们的孩子分别对应的是a、b、c.
(1)若主持人分别从三位家长和三位孩子中各选一人参加游戏,恰好是A、a的概率是多少(直接写出答案)
(2)若主持人先从三位家长中任选两人为一组,再从孩子中任选两人为一组,四人共同参加游戏,恰好是两对家庭成员的概率是多少.(画出树状图或列表)