下列为某校初三参加的“迎青奥”知识能力竞赛的25位同学的成绩:
78,86,98,90,95, 88,94,80,89,77, 87,73,65,84,87,
96,84,74,98,86, 83,67,88,68,85.
(1)完成下表:
(2)补全频数分布直方图;
(3)若超过均分的将获奖,请计算本次竞赛获奖的比例.
若关于 的一元二次方程
的一元二次方程 的常数项为0,求
的常数项为0,求 的值是多少?
的值是多少?
已知:如图所示的一张矩形纸片 ,将纸片折叠一次,使点
,将纸片折叠一次,使点 与
与 重合,再展开,折痕
重合,再展开,折痕 交
交 边于
边于 ,交
,交 边于
边于 ,分别连接
,分别连接 和
和 .
.
(1)求证:四边形 是菱形.
是菱形.
(2)若 ,△
,△ 的面积为
的面积为 ,求△
,求△ 的周长.
的周长.
(3)在线段 上是否存在一点
上是否存在一点 ,使得
,使得 ?若存在,请说明点
?若存在,请说明点 的位置,并予以证明;若不存在,请说明理由.
的位置,并予以证明;若不存在,请说明理由.
在一个不透明的纸箱里装有红、黄、蓝三种颜色的小球,它们除颜色外完全相同,其中红球有2个,黄球有1个,蓝球有1个.现有一张电影票,小明和小亮决定通过摸球游戏定输赢(赢的一方得电影票).游戏规则是:两人各摸1次球,先由小明从纸箱里随机摸出1个球,记录颜色后放回,将小球摇匀,再由小亮随机摸出1个球并记录颜色.若两人摸到的球颜色相同,则小明赢,否则小亮赢.这个游戏规则对双方公平吗?请你利用树状图或列表法说明理由.
如图,在一次夏令营活动中,小明从营地 出发,沿北偏东60°方向走了
出发,沿北偏东60°方向走了 m到达
m到达 点,然后再沿北偏西
点,然后再沿北偏西 方向走了
方向走了 到达目的地
到达目的地 点.求:
点.求:
(1) 两地之间的距离;
两地之间的距离;
(2)确定目的地C在营地 的什么方向.
的什么方向.
如图,防洪大堤的横断面是梯形,背水坡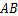 的坡比
的坡比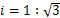 (指坡面的铅直高度与水平宽度的比),且
(指坡面的铅直高度与水平宽度的比),且 .身高为
.身高为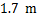 的小明站在大堤
的小明站在大堤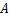 点,测得高压电线杆端点
点,测得高压电线杆端点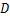 的仰角为
的仰角为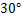 .已知地面
.已知地面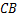 宽
宽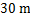 ,求高压电线杆
,求高压电线杆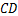 的高度(结果保留三个有效数字,
的高度(结果保留三个有效数字, 1.732).
1.732).