(本题10分)对于平面直角坐标系中的任意两点P1(x1,y1),P2(x2,y2),我们把|x1-x2|+|y1-y2|叫做P1、P2两点间的直角距离,记作d(P1,P2).
(1)令P0(2,-3),O为坐标原点,则d(O,P0)= ;
(2)已知O为坐标原点,动点P(x,y)满足d(O,P)=1,请写出x与y之间满足的关系式,并在所给的直角坐标系中画出所有符合条件的点P所组成的图形;
(3)设P0(x0,y0)是一定点,Q(x,y)是直线y=ax+b上的动点,我们把d(P0,Q)的最小值叫做P0到直线y=ax+b的直角距离.若P(a,-3)到直线y=x+1的直角距离为6,求a的值.
已知一口袋中放有黑白两种颜色的球,其中黑色球6个,白色球若干,为了估算白球的个数,可以每次从中取出一球,共取50次,如果其中有白球45个,则可估算其中白球个数为多少个?简要写出你的计算过程.
一个不透明的口袋中,装有30个外形及大小一样的球,颜色有红、黄二种,设计一套方案,估算两种颜色的球各多少个?
随意掷一枚骰子得到“5点的概率”是多少?设计一个方案来证明你的结论.
如图,已知正方形ABCD,点E是BC上一点,以AE为边作正方形AEFG。
(1)连结GD,求证△ADG≌△ABE;
(2)连结FC,求证∠FCN=45°;
(3)请问在AB边上是否存在一点Q,使得四边形DQEF是平行四边形?若存在,请证明;若不存在,请说明理由。
如图,已知△ABC中,AB=AC,AD是∠BAC的平分线,AE是∠BAC的外角平分线,CE⊥AE于点E。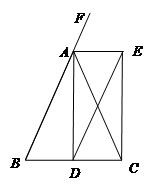
(1)求证:四边形ADCE为矩形;
(2)求证:四边形ABDE为平行四边形。