（本题8分）如图，一次函数 y="kx+b" 的图象与反比例函数y=
的图象交于 A（﹣2，1），B（1，n）两点．
（1)试确定上述反比例函数和一次函数的表达式；
（2)连OB，在x轴上取点C，使BC=BO，并求△OBC的面积.
杂技团进行杂技表演，演员从跷跷板右端A处弹跳到人梯顶端椅子B处，其身体（看成一点）的路线是抛物线
的一部分，如图．
（1）求演员弹跳离地面的最大高度；
（2）已知人梯高BC＝3．4米，在一次表演中，人梯到起跳点A的水平距离是4米，问这次表演是否成功？请说明理由．
如图所示，在平面直角坐标系中，一次函数y=kx+1，的图象与反比例函数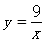
的图象在第一象限相交于点A，过点A分别作x 轴、y轴的垂线，垂足为点B、C．如果四边形OBAC是正方形，求一次函数的关系式．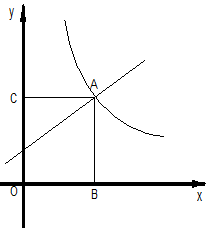
已知二次函数当x=1时，y有最大值为5，且它的图象经过点（2，3），求这个函数的关系式．
与
成反比例，当
＝2时，＝－1，求函数解析式和自变量的取值范围。
如图1，在平面直角坐标系中，二次函数y=ax2+bx+c（a≠0）的图象的顶点为D点，与y轴交于C点，与x轴交于A、B两点，A点在原点的左侧，B点的坐标为（3，0），A点坐标为（-1,0）OB＝OC ，
（1）求这个二次函数的表达式．
（2）经过C、D两点的直线，与x轴交于点E，在该抛物线上是否存在这样的点F，使以点A、C、E、F为顶点的四边形为平行四边形？若存在，请求出点F的坐标；若不存在，请说明理由．
（3）如图2，若点G（2，y）是该抛物线上一点，点P是直线AG下方的抛物线上一动点，当点P运动到什么位置时，△APG的面积最大？求出此时P点的坐标和△APG的最大面积.
图1图2