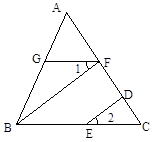(本题10分)某工厂设门市部专卖某产品,该产品每件成本30元,从开业一段时间的每天销售统计中,随机抽取一部分情况如下表所示:
| 销售单位(元) |
50 |
60 |
70 |
75 |
80 |
85 |
… |
| 日销售量(件) |
300 |
240 |
180 |
150 |
120 |
90 |
… |
假设每天定的售价是不变的,且每天销售情况均服从这种规律.
(1)观察表格判断日销售量与销售价格之间的函数关系,并求出函数关系式;
(2)门市部原设定两名销售员,但当销售量较大时,在每天售出量超过198件时,则必须增派一名营业员才能保证营业有序进行.设营业员每人每天工资为40元,求每件产品应定价多少元,才能使每天门市部纯利润最大?(纯利润=总销售﹣成本﹣营业员工资)
化简:
探究与发现:
如图(1)所示的图形,像我们常见的学习用品——圆规.我们不妨把这样图形叫做“规形图”,那么在这一个简单的图形中,到底隐藏了哪些数学知识呢?下面就请你发挥你的聪明才智,解决以下问题:
(1)观察“规形图”(图1),试探究∠BDC与∠A、∠B、∠C之间的关系,并说明理由;
(2)请你直接利用以上结论,解决以下三个问题:
①如图(2),把一块三角尺XYZ放置在△ABC上,使三角尺的两条直角边XY、XZ恰好经过点B、C,若∠A=50°,则∠ABX+∠ACX =__________°;
②如图(3),DC平分∠ADB,EC平分∠AEB,若∠DAE=50°,∠DBE=130°,则∠DCE= __________°;
③如图(4),∠ABD、∠ACD的10等分线相交于点G1、G2…、G9,若∠BDC=140°,∠BG5C=105°,求∠A的度数.
你能求 的值吗?从简单的情形入手,通过计算发现:①
的值吗?从简单的情形入手,通过计算发现:①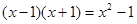 ; ②
; ② ;③
;③ ;……
;……
(1)按此规律可以得到: =____________;
=____________;
(2)请你利用上面的结论,计算: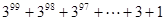 .
.
现有两块大小相同的直角三角板△ABC、△DEF,∠ACB=∠DFE=90°,
∠A=∠D=30°.
(1)将这两块三角板摆成如图①的形式,使B、F、E、A在同一条直线上,点C在边DF上,DE与AC相交于点G,试求∠AGD的度数;
(2)将图①中的△ABC固定,把△DEF绕着点F逆时针旋转成如图②的形式,当旋转的角度等于多少度时,DF∥AC? 并说明理由.
如图,在△ABC中,BF是高,点E、D分别在BC、AC上,且ED⊥AC,∠1=∠2,试判断GF与BC的位置关系,并说明理由.