（本题14分）已知在平面直角坐标系xOy中，O是坐标原点，以P（1，1）为圆心的⊙P与x轴、y轴分别相切于点M和点N，点F从点M出发，沿x轴正方向以每秒1个单位长度的速度运动，连接PF，过点P作PE⊥PF交y轴于点E，设点F运动的时间是t秒（t＞0）
（1）若点E在y轴的负半轴上（如图所示），求证：PE=PF；
（2）在点F运动过程中，设OE=a，OF=b，试用含a的代数式表示b；
（3）作点F关于点M的对称点F′，经过M、E和F′三点的抛物线的对称轴交x轴于点Q，连接QE．在点F运动过程中，是否存在某一时刻，使得以点Q、O、E为顶点的三角形与以点P、M、F为顶点的三角形相似？若存在，请直接写出t的值；若不存在，请说明理由．
如图，在平面直角坐标系 xOy中，反比例函数 y＝ 的图象与一次函数 y＝ k（ x﹣2）的图象交点为 A（3，2）， B（ x， y）．
（1）求反比例函数与一次函数的解析式及 B点坐标；
（2）若 C是 y轴上的点，且满足△ ABC的面积为10，求 C点坐标．
如图，在平面直角坐标系中， O（0，0）， A（0，﹣6）， B（8，0）三点在⊙ P上， M为劣弧的 中点．
（1）求圆的半径及圆心 P的坐标；
（2）求证： AM是∠ OAB的平分线；
（3）连接 BM并延长交 y轴于点 N，求 N， M点的坐标．
如图，一块长5米宽4米的地毯，为了美观设计了两横、两纵的配色条纹（图中阴影部分），已知配色条纹的宽度相同，所占面积是整个地毯面积的 ．
（1）求配色条纹的宽度；
（2）如果地毯配色条纹部分每平方米造价200元，其余部分每平方米造价100元，求地毯的总造价．
为有效开发海洋资源，保护海洋权益，我国对南海诸岛进行了全面调查，一测量船在 A岛测得 B岛在北偏西30°， C岛在北偏东15°，航行100海里到达 B岛，在 B岛测得 C岛在北偏东45°，求 B， C两岛及 A， C两岛的距离（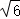 
≈2.45，结果保留到整数）
下表是博文学校初三•一班慧慧、聪聪两名学生入学以来10次数学检测成绩（单位：分）．
|
慧慧 |
116 |
124 |
130 |
126 |
121 |
127 |
126 |
122 |
125 |
123 |
|
聪聪 |
122 |
124 |
125 |
128 |
119 |
120 |
121 |
128 |
114 |
119 |
回答下列问题：
（1）分别求出慧慧和聪聪成绩的平均数；
（2）分别计算慧慧和聪聪两组数据的方差；
（3）根据（1）（2）你认为选谁参加全国数学竞赛更合适？并说明理由；
（4）由于初三•二班、初三•三班和初三•四班数学成绩相对薄弱，学校打算派慧慧和聪聪分别参加三个班的数学业余辅导活动，求两名学生分别在初三•二班和初三•三班的概率．