直角三角板ABC中,∠A=30°,BC=2 将其绕直角顶点C逆时针旋转一个角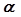 (
(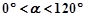 且
且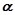 ≠ 90°),得到Rt△
≠ 90°),得到Rt△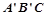 ,
,
(1)如图1,当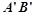 边经过点B时,求旋转角
边经过点B时,求旋转角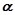 的度数;
的度数;
(2)在三角板旋转的过程中,边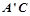 与AB所在直线交于点D,过点 D作DE∥
与AB所在直线交于点D,过点 D作DE∥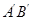 交
交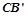 边于点E,联结BE
边于点E,联结BE
①当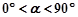 时,设
时,设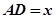 ,
,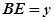 ,求
,求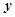 与
与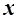 之间的函数解析式及
之间的函数解析式及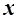 取值范围;
取值范围;
②当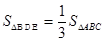 时,求
时,求 的长
的长
如图,抛物线y=ax2+bx+c(a≠0)与y轴交于点C(0,4),与x轴交于点A和点B,其中点A的坐标为(﹣2,0),抛物线的对称轴x=1与抛物线交于点D,与直线BC交于点E.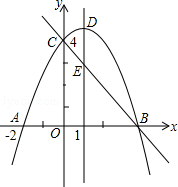
(1)求抛物线的解析式;
(2)若点F是直线BC上方的抛物线上的一个动点,是否存在点F使四边形ABFC的面积为17,若存在,求出点F的坐标;若不存在,请说明理由;
某企业生产的一批产品上市后30天内全部售完,调查发现,国内市场的日销售量为y1(吨)与时间t(t为整数,单位:天)的关系如图1所示的抛物线的一部分,而国外市场的日销售量y2(吨)与时间t,t为整数,单位:天)的关系如图2所示.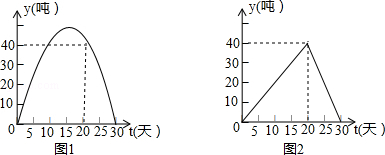
(1)求y1与时间t的函数关系式及自变量t的取值范围,并写出y2与t的函数关系式及自变量t的取值范围;
(2)设国内、国外市场的日销售总量为y吨,直接写出y与时间t的函数关系式,当销售第几天时,国内、外市场的日销售总量最早达到75吨?
(3)判断上市第几天国内、国外市场的日销售总量y最大,并求出此时的最大值.
甲、乙两人用手指玩游戏,规则如下:①每次游戏时,两人同时随机地各伸出一根手指;②两人伸出的手指中,大拇指只胜食指、食指只胜中指、中指只胜无名指、无名指只胜小拇指、小拇指只胜大拇指,否则不分胜负.依据上述规则,当甲、乙两人同时随机地各伸出一根手指时,
(1)用树状图(或表格)表示所有情况;
(2)求甲伸出小拇指取胜的概率;
(3)求乙取胜的概率.
在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=x(m).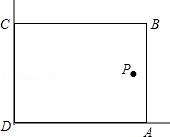
(1)若花园的面积为187m2,求x的值;
(2)若在P处有一棵树与墙CD,AD的距离分别是16m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积S的最大值.
请你依据下面图框中的寻宝游戏规则,探究“寻宝游戏”的奥秘: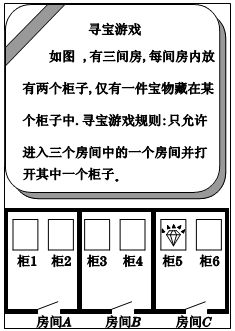
(1)用树状图(或表格)表示出所有可能的寻宝情况;
(2)求在寻宝游戏中胜出的概率.