请你依据下面图框中的寻宝游戏规则,探究“寻宝游戏”的奥秘: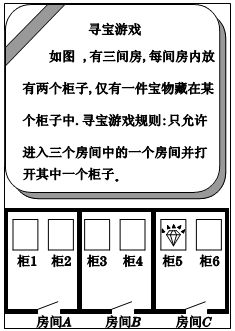
(1)用树状图(或表格)表示出所有可能的寻宝情况;
(2)求在寻宝游戏中胜出的概率.
如图所示,已知梯形ABCD中,AD∥BC,且AD<BC,N、M分别为AC、BD的中点,
求证:(1)MN∥BC;(2)MN=  (BC-AD).
(BC-AD).
如图,△ABC中,点O是AC边上的一动点,过O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
(1)求证:OE=OF;
(2)当点O运动到何处时,四边形AECF是矩形,并证明你的结论;
如图,四边形ABCD中,∠DAB=∠BCD=90°,M为BD中点,N为AC中点,求证:MN⊥AC.
如图所示,在△ABC,∠C=90°,AC=BC,AD是∠BAC的平分线,DE⊥AB于E点,已知AB=10cm,求△DEB的周长。
如图,ABCD是菱形,对角线AC与BD相交于O,∠ACD=30°,BD=6.
(1)求证:△ABD是正三角形;
(2)求AC的长(结果可保留根号).