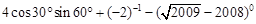某超市销售一种商品,成本每千克40元,规定每千克售价不低于成本,且不高于80元,经市场调查,每天的销售量(千克)与每千克售价(元满足一次函数关系,部分数据如下表:
售价(元千克) |
50 |
60 |
70 |
销售量(千克) |
100 |
80 |
60 |
(1)求与之间的函数表达式;
(2)设商品每天的总利润为(元,求与之间的函数表达式(利润收入成本);
(3)试说明(2)中总利润随售价的变化而变化的情况,并指出售价为多少元时获得最大利润,最大利润是多少?
如图,二次函数y= -x2+ax+b的图象与x轴交于A(- ,0)、B(2,0)两点,且与y轴交于点C.
,0)、B(2,0)两点,且与y轴交于点C.
(1)求该拋物线的解析式,并判断△ABC的形状;
(2)在x轴上方的拋物线上有一点D,且以A、C、D、B四点为顶点的四边形是等腰梯形,请直接写出D点的坐标;
(3)在拋物线上存在点P,使得以A、C、B、P四点为顶点的四边形是直角梯形,求出P点的坐标.
将如图所示的牌面数字分别是1,2,3,4的四张扑克牌背面朝上,洗匀后放在桌面上.
(1)从中随机抽出一张牌,牌面数字是偶数的概率是;
(2)从中随机抽出二张牌,两张牌牌面数字的和是5的概率是;
(3)先从中随机抽出一张牌,将牌面数字作为十位上的数字,然后将该牌放回并重新洗匀,再随机抽取一张,将牌面数字作为个位上的数字,请用画树状图或列表的方法求组成的两位数恰好是4的倍数的概率.
商场某种商品平均每天可销售30件,每件盈利50元。为了尽快减少库存,商场决定采取适当的降价措施。经调查发现,每件商品每降价1元,商场平均每天可多售出2件。每件商品降价多少元时,商场日盈利可达到2100元?为获得最大利润,商场该商品应降价多少元?
如图,某幼儿园为了加强安全管理,决定将园内的滑滑板的倾角由45º降为30º,已知原滑滑板AB的长为5米,点D、B、C在同一水平地面上.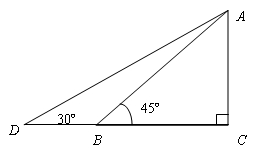
(1)改善后滑滑板会加长多少?(精确到0.01)
(2)若滑滑板的正前方能有3米长的空地就能保证安全,原滑滑板的前方有6米长的空地,像这样改造是否可行?说明理由 (参考数据: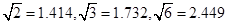 )
)
(1)解方程: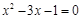 .
.
(2)