(本小题满分14分)在直角坐标系 中,曲线
中,曲线 上的点均在圆
上的点均在圆 外,且对
外,且对 上任意一点
上任意一点 ,
, 到直线
到直线 的距离等于该点与圆
的距离等于该点与圆 上点的距离的最小值.
上点的距离的最小值.
(1)求曲线 的方程;
的方程;
(2)设 为圆
为圆 外一点,过
外一点,过 作圆
作圆 的两条切线,分别与曲线
的两条切线,分别与曲线 相交于点
相交于点 和
和 .证明:当
.证明:当 在直线
在直线 上运动时,四点
上运动时,四点
 的纵坐标之积为定值.
的纵坐标之积为定值.
(本小题满分14分)已知函数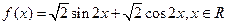 .
.
(I)求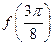 的值;
的值;
(II)求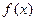 的最大值和最小正周期;
的最大值和最小正周期;
(Ⅲ)若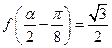 ,
,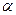 是第二象限的角,求
是第二象限的角,求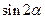 .
.
(本小题满分14分)
已知函数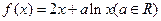
(Ⅰ)请研究函数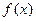 的单调性;
的单调性;
(Ⅱ)若函数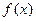 有两个零点,求实数
有两个零点,求实数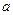 的取值范围;
的取值范围;
(Ⅲ)若定义在区间D上的函数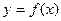 对于区间D上的任意两个值x1、x2总有以下不等式
对于区间D上的任意两个值x1、x2总有以下不等式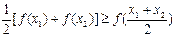 成立,则称函数
成立,则称函数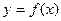 为区间D上的“凹函数”.若函
为区间D上的“凹函数”.若函
数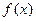 的最小值为
的最小值为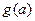 ,试判断函数
,试判断函数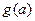 是否为“凹函数”,并对你的判断加以证明.
是否为“凹函数”,并对你的判断加以证明.
(本小题满分14分)
已知双曲线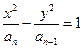 的一个焦点为(
的一个焦点为(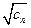 ,0),一条渐近线方程为
,0),一条渐近线方程为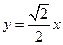 ,其中
,其中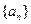
是以4为首项的正数数列,记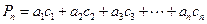 .
.
(Ⅰ)求数列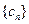 的通项公式;
的通项公式;
(Ⅱ)若数列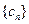 的前n项的和为Sn,求
的前n项的和为Sn,求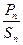 ;
;
(Ⅲ)若不等式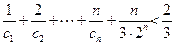 +
+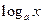 (a>0,且a≠1)对一切自然数n恒成立,求实数x的取值范围.
(a>0,且a≠1)对一切自然数n恒成立,求实数x的取值范围.
在直角坐标系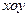 中,动点
中,动点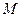 到两圆
到两圆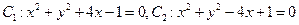 的圆心
的圆心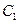 和
和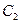 的距离的和等于
的距离的和等于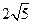 .
.
(Ⅰ) 求动点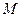 的轨迹方程;
的轨迹方程;
(Ⅱ) 以动点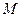 的轨迹与
的轨迹与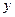 轴正半轴的交点C为直角顶点作此轨迹的内接等腰直角三角形ABC,试问:这样的等腰直角三角形是否存在?若存在,有几个?若不存在,请说明理由.
轴正半轴的交点C为直角顶点作此轨迹的内接等腰直角三角形ABC,试问:这样的等腰直角三角形是否存在?若存在,有几个?若不存在,请说明理由.
(本小题满分14分)
如图5, 是棱长为2 cm的正方体.
是棱长为2 cm的正方体.
(I) 求多面体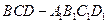 的体积;
的体积;
(II) 求点A到平面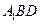 的距离;
的距离;
(Ⅲ) 求证:平面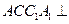 平面
平面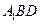 .
.