已知数列{}满足+=2n+1 （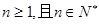
）
（1）求出，，的值；
（2）由（1）猜想出数列{}的通项公式，并用数学归纳法证明．
（本小题满分13分）已知集合
，集合
（Ⅰ）若
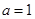，求
；
（Ⅱ）若A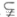
B，求实数
的取值范围．
（本小题满分10分 ）选修4—5：不等式选讲
已知
，且关于
的不等式
的解集为
.
（Ⅰ）求
的值；
（Ⅱ）若
，
均为正实数，且满足
，求
的最小值.
（本小题满分10分 ）选修4—4：坐标系与参数方程
在直角坐标系
中，直线
的参数方程为
为参数），以该直角坐标系的原点
为极点，
轴的正半轴为极轴的极坐标系下，圆
的方程为
．
（Ⅰ）求直线的普通方程和圆的圆心的极坐标；
（Ⅱ）设直线和圆的交点为
、
，求弦
的长．
（本小题满分10分 ）选修4—1：几何证明选讲
如图，
为⊙
的直径，直线
与⊙相切于点
，
垂直于点
，
垂直于点
，
垂直于点
，连接
，
.
证明：（Ⅰ）
；
（Ⅱ）
．
（本小题满分12分）已知函数
．
（I）讨论函数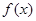
的单调区间；
（II）当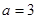
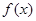时，若函数在区间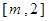
上的最大值为
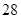，求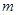
的取值范围．