（本小题满分10分）设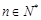
且
，集合
的所有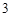
个元素的子集记为
．
（1）求集合中所有元素之和
；
（2）记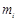
为
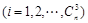中最小元素与最大元素之和，求
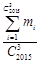的值．
某公司为了实现2011年1000万元的利润的目标，准备制定一个激励销售人员的奖励方案：销售利润达到10万元时，按销售利润进行奖励，且奖金数额y（单位：万元）随销售利润x（单位：万元）的增加而增加，但奖金数额不超过5万元，同时奖金数额不超过利润的25%，现有二个奖励模型：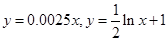
，问其中是否有模型能完全符合公司的要求？说明理由。（解题提示：公司要求的模型只需满足：当
时，①函数为增函数；②函数的最大值不超过5；③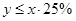
，参考数据：
）
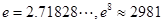已知函数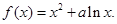
（1）当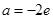
时，求函数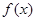
的单调区间；
（2）若函数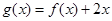
在[1，4]上是减函数，求实数a的取值范围。
（本小题满分12分）
已知
平面ABC，
，AC=CB=AD=2，E是DC的中点，F是AB的中点。
（1）证明：
；
（2）求二面角C—DB—A的正切值。
已知数列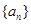
的前n项和为
，
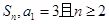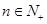，满足
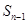是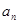
与-3的等差中项。
（1）求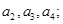
（2）求数列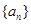的通项公式。
已知函数
（1）求函数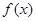
的最小值和最小正周期；
（2）求函数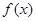的单调递增区间。