(本小题满分16分) 已知椭圆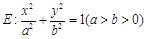 过点
过点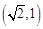 ,离心率为
,离心率为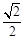 .
.
(1)若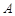 是椭圆
是椭圆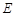 的上顶点,
的上顶点,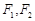 分别是左右焦点,直线
分别是左右焦点,直线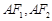 分别交椭圆于
分别交椭圆于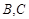 ,直线
,直线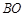 交
交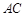 于D,求证
于D,求证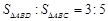 ;
;
(2)若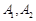 分别是椭圆
分别是椭圆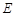 的左右顶点,动点
的左右顶点,动点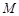 满足
满足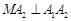 ,且
,且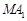 交椭圆
交椭圆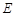 于点
于点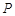 .
.
求证: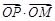 为定值.
为定值.
海关对同时从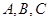 三个不同地区进口的某种商品进行抽样检测,从各地区进口此种商品的数量(单位:件)如下表所示,工作人员用分层抽样的方法从这些商品中共抽取6件进行检测.
三个不同地区进口的某种商品进行抽样检测,从各地区进口此种商品的数量(单位:件)如下表所示,工作人员用分层抽样的方法从这些商品中共抽取6件进行检测.
| 地区 |
 |
 |
 |
| 数量 |
50 |
150 |
100 |
(1)求这6件样品中来自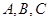 各地区商品的数量;
各地区商品的数量;
(2)若在这6件样品中随机抽取2件送往甲机构进一步检测,求这2件商品来自相同地区的概率.
在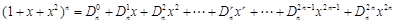 的展开式中,把
的展开式中,把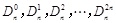 叫做三项式系数.
叫做三项式系数.
(1)当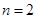 时,写出三项式系数
时,写出三项式系数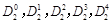 的值;
的值;
(2)类比二项式系数性质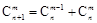
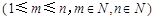 ,给出一个关于三项式系数
,给出一个关于三项式系数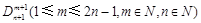 的相似性质,并予以证明;
的相似性质,并予以证明;
(3)求 的值.
的值.
(1)求证: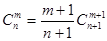 ;
;
(2)求和: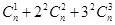
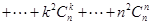 .
.
设有关于x的一元二次方程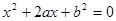 .
.
(1)若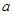 是从0,1,2,3四个数中任取的一个数,
是从0,1,2,3四个数中任取的一个数, 是从0,1,2三个数中任取的一个数,求上述方程有实根的概率.
是从0,1,2三个数中任取的一个数,求上述方程有实根的概率.
(2)若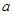 是从区间
是从区间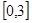 任取得一个数,
任取得一个数, 是从区间
是从区间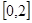 任取的一个数,求上述方程有实根的概率.
任取的一个数,求上述方程有实根的概率.
已知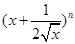 的展开式中前三项的系数成等差数列.
的展开式中前三项的系数成等差数列.
(1)求 的值;
的值;
(2)求展开式中系数最大的项.