已知椭圆 的中心在原点,焦点在
的中心在原点,焦点在 轴上,它的一个顶点恰好经过抛物线
轴上,它的一个顶点恰好经过抛物线 的准线,且经过点
的准线,且经过点 .
.
(1)求椭圆 的方程;
的方程;
(2) 若直线
若直线 的方程为
的方程为 .
. 是经过椭圆左焦点
是经过椭圆左焦点 的任一弦,设直线
的任一弦,设直线 与直线
与直线 相交于点
相交于点 ,记
,记 的斜率分别为
的斜率分别为 .试探索
.试探索 之间有怎样的关系式?给出证明过程.
之间有怎样的关系式?给出证明过程.
(本小题满分14分)如图,在四棱锥P—ABCD中,PD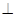 底面ABCD,底面ABCD是正方形,PD=DC,E、F分别为AB、PB的中点。
底面ABCD,底面ABCD是正方形,PD=DC,E、F分别为AB、PB的中点。
(1)求证:EF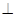 CD;
CD;
(2)求DB与平面DEF所成角的正弦值;
(3)在平面PAD内求一点G,使GF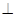 平面PCB,并
平面PCB,并
证明你的结论。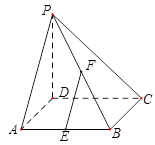
(本小题满分13分)运货卡车以每小时x千米的速度匀速行驶130千米(50≤x≤100)
(单位:千米/小时).假设汽油的价格是每升2元,而汽车每小时耗油(2+)升,
司机的工资是每小时14元.
(1)求这次行车总费用y关于x的表达式;
(2)当x为何值时,这次行车的总费用最低,并求出最低费用的值.
(本小题满分13分)在△ABC中,a、b、c分别是角A、B、C的对边,且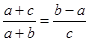 ,
,
(1)求角B的大小;
(2)若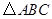 最大边的边长为
最大边的边长为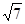 ,且
,且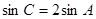 ,求最小边长.
,求最小边长.
(本小题满分13分)已知 ,命题
,命题 “函数
“函数 在
在 上单调递减”,
上单调递减”,
命题 “关于
“关于 的不等式
的不等式 对一切的
对一切的 恒成立”,若
恒成立”,若 为假命题,
为假命题, 为真命题,求实数
为真命题,求实数 的取值范围.
的取值范围.
. (本小题满分13分)已知数列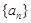 的前
的前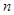 项和为
项和为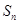 ,且
,且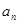 是
是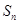 与2的等差中项,
与2的等差中项,
⑴求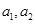 的值;
的值;
⑵求数列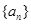 的通项公式。
的通项公式。