(本小题满分12分)若函数f(x)=x2-(2a-4)x-3在[1,3]上的最小值是g(a),求g(a)的函数表达式.
(本小题满分12分)已知函数f(x)= 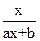 (a,b为常数,且a≠0)满足f(2)= 1且方程f(x)= x有唯一解,求函数f(x)的解析式
(a,b为常数,且a≠0)满足f(2)= 1且方程f(x)= x有唯一解,求函数f(x)的解析式
本小题满分12分)某商场购进一批单价为16元的日用品,经试验发现,若按每件20元的价格销售时,每月能卖360件,若按每件25元的价格销售时,每月能卖210件,假定每月销售件数y( 件)是价格x(元/件)的
件)是价格x(元/件)的 一次函数.
一次函数.
(1)试求y与x之间的关系式;
(2)在商品不积压,且不考虑其他因素的条件下,问销售价格定为多少时,才能使每月获得最大利润?每月的最大利润是多少?
集合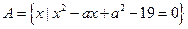 ,
,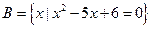 ,
,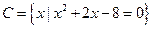 满足
满足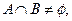 ,
,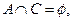 求实数
求实数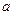 的值。
的值。
(本题满分12分)设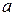 为实数,函数
为实数,函数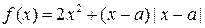 .
.
(1)若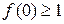 ,求
,求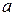 的取值范围;
的取值范围;
(2)求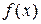 的最小值;
的最小值;
(3)设函数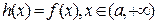 ,直接写出(不需给出演算步骤)不等式
,直接写出(不需给出演算步骤)不等式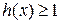 的解集.
的解集.