（本小题满分12分） 一个社会调查机构就某社区居民的月收入调查了10 000人，并根据所得数据画了样本的频率分布直方图（如图）.
（1）为了分析居民的收入与年龄、学历、职业等方面的关系，要从这10 000人中再用分层抽样方法抽出100人作进一步调查，求月收入在
（元）段应抽出的人数；
（2）为了估计该社区3个居民中恰有2个月收入在
（元）的概率，采用随机模拟的方法：先由计算器产生0到9之间取整数值的随机数，我们用0，1，2，3，4表示收入在（元）的居民，剩余的数字表示月收入不在（元）的居民；再以每三个随机数为一组，代表统计的结果，经随机模拟产生了20组随机数如下：
907 966 191 925 271 932 812 458 569 683 431 257 393 027 556 488 730 113 537 989
据此估计，计算该社区3个居民中恰好有2个月收入在（元）的概率.
函数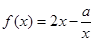
的定义域为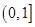
（a为实数），
（1）当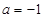
时，求函数
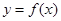的值域。
（2）若函数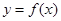在定义域上是减函数，求a的取值范围
（3）求函数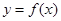在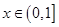
上的最大值及最小值。
某商品一年内出厂价格在6元的基础上按月份随正弦曲线波动，已知3月份达到最高价格8元，7月份价格最低为4元.该商品在商店内的销售价格在8元基础上按月份随正弦曲线波动，5月份销售价格最高为10元，9月份销售价最低为6元.
（1）试分别建立出厂价格、销售价格的模型，并分别求出函数解析式;
（2）假设商店每月购进这种商品m件，且当月销完，试写出该商品的月利润函数；
（3）求该商店月利润的最大值.（定义运算
若函数
（
）在
上的最大值为23，求a的值.
已知tanα，
是关于x的方程x2-kx+k2-3=0的两实根，且3π＜α＜
π，
求cos(3π+α)-sin(π+α)的值.
(1)已知角α的终边经过点P(4，-3)，求2sinα+cosα的值；
(2)已知角α的终边经过点P(4a，-3a)(a≠0)，求2sinα+cosα的值；