（本题10分）问题背景：如图1：在四边形ABCD中，ABAD-优题课

（本题10分）问题背景：如图1：在四边形ABCD中，AB=AD，∠BAD=120°，∠B=∠ADC=90°．E，F分别是BC，CD上的点．且∠EAF=60°．探究图中线段BE，EF，FD之间的数量关系．
小王同学探究此问题的方法是，延长FD到点G．使DG=BE．连结AG，先证明△ABE≌△ADG，再证明△AEF≌△AGF，可得出结论，他的结论应是；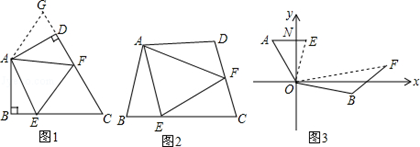

探索延伸：如图2，若在四边形ABCD中，AB=AD，∠B+∠D=180°．E，F分别是BC，CD上的点，且∠EAF=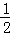∠BAD，上述结论是否仍然成立，并说明理由；
实际应用：如图3，在某次军事演习中，舰艇甲在指挥中心（O处）北偏西30°的A处，舰艇乙在指挥中心南偏东70°的B处，并且两舰艇到指挥中心的距离相等，接到行动指令后，舰艇甲向正东方向以60海里/小时的速度前进，舰艇乙沿北偏东50°的方向以80海里/小时的速度前进．1．5小时后，指挥中心观测到甲、乙两舰艇分别到达E，F处，且两舰艇之间的夹角为70°，试求此时两舰艇之间的距离．

科目数学题型解答题难度中等

知识点：三角形的五心

有2部不同的电影 $A$ 、 $B$ ，甲、乙、丙3人分别从中任意选择1部观看．

（1）求甲选择 $A$ 电影的概率；

（2）求甲、乙、丙3人选择同1部电影的概率（请用画树状图的方法给出分析过程，并求出结果）．

如图，在 $▱ ABCD$ 中，点 $E$ 、 $F$ 分别在边 $CB$ 、 $AD$ 的延长线上，且 $BE = DF$ ， $EF$ 分别与 $AB$ 、 $CD$ 交于点 $G$ 、 $H$ ．求证： $AG = CH$ ．

某市举行“传承好家风”征文比赛，已知每篇参赛征文成绩记 $m$ 分 $(60 ⩽ m ⩽ 100)$ ，组委会从1000篇征文中随机抽取了部分参赛征文，统计了它们的成绩，并绘制了如图不完整的两幅统计图表．

征文比赛成绩频数分布表

分数段	频数	频率
$60 ⩽ m < 70$	38	0.38
$70 ⩽ m < 80$	$a$	0.32
$80 ⩽ m < 90$	$b$	$c$
$90 ⩽ m ⩽ 100$	10	0.1
合计		1

请根据以上信息，解决下列问题：

（1）征文比赛成绩频数分布表中 $c$ 的值是　　；

（2）补全征文比赛成绩频数分布直方图；

（3）若80分以上（含80分）的征文将被评为一等奖，试估计全市获得一等奖征文的篇数．

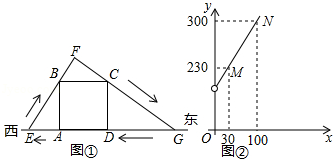
如图①，直线 $l$ 表示一条东西走向的笔直公路，四边形 $ABCD$ 是一块边长为100米的正方形草地，点 $A$ ， $D$ 在直线 $l$ 上，小明从点 $A$ 出发，沿公路 $l$ 向西走了若干米后到达点 $E$ 处，然后转身沿射线 $EB$ 方向走到点 $F$ 处，接着又改变方向沿射线 $FC$ 方向走到公路 $l$ 上的点 $G$ 处，最后沿公路 $l$ 回到点 $A$ 处．设 $AE = x$ 米（其中 $x > 0)$ ， $GA = y$ 米，已知 $y$ 与 $x$ 之间的函数关系如图②所示，

（1）求图②中线段 $MN$ 所在直线的函数表达式；

（2）试问小明从起点 $A$ 出发直至最后回到点 $A$ 处，所走过的路径（即 $ΔEFG)$ 是否可以是一个等腰三角形？如果可以，求出相应 $x$ 的值；如果不可以，说明理由．

问题1：如图①，在 $ΔABC$ 中， $AB = 4$ ， $D$ 是 $AB$ 上一点（不与 $A$ ， $B$ 重合）， $DE / / BC$ ，交 $AC$ 于点 $E$ ，连接 $CD$ ．设 $ΔABC$ 的面积为 $S$ ， $ΔDEC$ 的面积为 $S'$ ．

（1）当 $AD = 3$ 时， $\frac{S'}{S} =$ 　　；

（2）设 $AD = m$ ，请你用含字母 $m$ 的代数式表示 $\frac{S'}{S}$ ．

问题2：如图②，在四边形 $ABCD$ 中， $AB = 4$ ， $AD / / BC$ ， $AD = \frac{1}{2} BC$ ， $E$ 是 $AB$ 上一点（不与 $A$ ， $B$ 重合）， $EF / / BC$ ，交 $CD$ 于点 $F$ ，连接 $CE$ ．设 $AE = n$ ，四边形 $ABCD$ 的面积为 $S$ ， $ΔEFC$ 的面积为 $S'$ ．请你利用问题1的解法或结论，用含字母 $n$ 的代数式表示 $\frac{S'}{S}$ ．