如右图所示,光滑的水平面AB与半径为R="0.32" m的光滑竖直半圆轨道BCD在B点相切,D为轨道最高点.用轻质细线连接甲、乙两小球,中间夹一轻质弹簧,弹簧与甲、乙两球不拴接.甲球的质量为m1="0.1" kg,乙球的质量为m2="0.3" kg,甲、乙两球静止在光滑的水平面上。现固定甲球,烧断细线,乙球离开弹簧后进入半圆轨道恰好能通过D点。重力加速度g取10 m/s2,甲、乙两球可看作质点。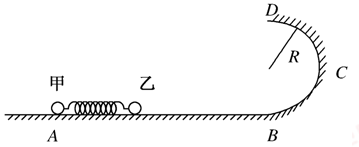
①试求细线烧断前弹簧的弹性势能;
②若甲球不固定,烧断细线,求乙球离开弹簧后进入半圆轨道能达到的最大高度;
屋檐上每隔相同的时间间隔滴下一滴水,当第5滴正欲滴下时,第1滴恰好到达地面,而第3滴与第2滴分别位于高为1 m的窗户的上下缘,如图所示.取g=10 m/s2,问: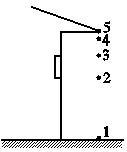
(1)此屋檐离地面多高?
(2)滴水的时间间隔是多少?
2008年北京奥运会场馆周围 80%~90%的路灯将利用太阳能发电技术来供电,奥运会90%的洗浴热水将采用全玻真空太阳能集热技术.科学研究发现太阳发光是由于其内部不断发生从氢核到氦核的核聚变反应,即在太阳内部4个氢核( H)转化成一个氦核(
H)转化成一个氦核( He)和两个正电子(
He)和两个正电子( e)并放出能量.已知质子质量mP=1.0073u,α粒子的质量mα=4.0015u,电子的质量me=0.0005u. 1u的质量相当于931.MeV的能量.
e)并放出能量.已知质子质量mP=1.0073u,α粒子的质量mα=4.0015u,电子的质量me=0.0005u. 1u的质量相当于931.MeV的能量.
(1)写出该热核反应方程;
(2)一次这样的热核反应过程中释放出多少MeV的能量?(结果保留四位有效数字)
容积为2L的烧瓶,在压强为1.0×105Pa时,用塞子塞住,此时温度为27℃,当把它加热到127℃时,塞子被打开了,稍过一会儿,重新把盖子塞好,停止加热并使它逐渐降温到27℃,求:
(1)塞子打开前的最大压强;
(2)27℃时剩余空气的压强。
如图10所示,AB、CD是处在方向垂直纸面向里、磁感应强度为B1的匀强磁场的两条金属导轨(足够长),导轨宽度为d,导轨通过导线分别与平行金属板MN相连,有一与导轨垂直且始终接触良好的金属棒ab以某一速度沿着导轨做匀速直线运动。在y轴的右方有一磁感应强度为B2且方向垂直纸面向外的匀强磁场。现有一质量为m、电荷量为q的带正电粒子在M板由静止经过平行金属板MN,然后以垂直于y轴的方向从F处穿过y轴进入磁场,运动一段时间后打到x轴上的G处,并与x轴正向的夹角为60°;已知OG长为 ,不计粒子的重力。求:
,不计粒子的重力。求:
(1)试判断ab棒的运动方向
(2)金属棒ab做匀速直线运动速度的大小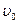 ?
?
如图9所示,光滑绝缘水平面上放置一均匀导体制成的正方形线框abcd,线框质量为m,电阻为R,边长为L。有一方向竖直向下的有界磁场,磁场的磁感应强度为B,磁场区宽度大于L,左右边界与ab边平行。线框在水平向右的拉力作用下垂直于边界线穿过磁场区。
(1)若线框以速度v匀速穿过磁场区,当线框ab边离开了磁场,而cd边还在磁场中时,求ab两点间的电势差;
(2)若线框从静止开始以恒定的加速度a运动,经过t1时间ab边开始进入磁场,求cd边将要进入磁场时回路的电功率;