(本小题满分12分)已知点 (
( )为平面直角坐标系
)为平面直角坐标系 中的点,点S为线段AB的中点,当
中的点,点S为线段AB的中点,当 变化时,点S形成轨迹
变化时,点S形成轨迹 .
.
(1)求S点的轨迹 的方程;
的方程;
(2)若点M的坐标为 ,是否存在直线
,是否存在直线 交S点的轨迹
交S点的轨迹 于P、Q两点,且使点
于P、Q两点,且使点 为
为 的垂心?若存在,求出直线
的垂心?若存在,求出直线 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
(本小题满分13分)
已知等差数列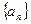 的公差为
的公差为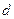 ,前
,前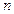 项和为
项和为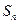 ,且满足
,且满足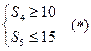 ,
,
(1)试用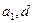 表示不等式组
表示不等式组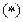 ,并在给定的坐标系中用阴影画出不等式组表示的平面区域;
,并在给定的坐标系中用阴影画出不等式组表示的平面区域;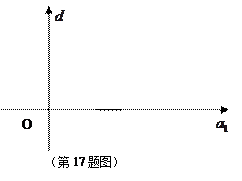 (2)求
(2)求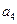 的最大值,并指出此时数列
的最大值,并指出此时数列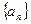 的公差
的公差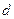 的值.
的值.
(本小题满分13分)
已知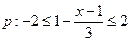 ,
, ,若
,若 是
是 的必要不充分条件,求实数
的必要不充分条件,求实数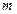 的取值范围.
的取值范围.
(本小题满分12分)
已知△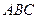 的周长为
的周长为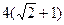 ,且
,且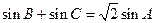 .
.
(1)求边长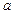 的值;
的值;
(2)若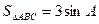 ,求角A的余弦值.
,求角A的余弦值.
(本小题满分14分)
已知数列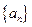 的各项满足:
的各项满足: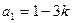
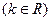 ,
,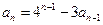 .
.
(1) 判断数列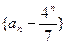 是否成等比数列;
是否成等比数列;
(2)求数列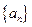 的通项公式;
的通项公式;
(3)若数列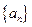 为递增数列,求
为递增数列,求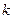 的取值范围.
的取值范围.
(本小题满分14分)
已知函数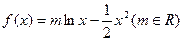
 满足
满足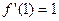 .
.
(1)求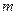 的值及函数
的值及函数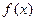 的单调区间;
的单调区间;
(2)若函数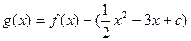 在
在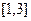 内有两
内有两 个零点,求实数
个零点,求实数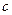 的取值范围.
的取值范围.