已知抛物线
，当
时，
值为正，当
或
时，值为负．
（1）求抛物线的解析式；
（2）若直线
与抛物线交于点
和
，求直线的解析式．
（3）设平行于轴的直线
和
分别交线段
于
、
，交抛物线于
、
，
①求
的取值范围；
②是否存在适当的值，使得四边形
是平行四边形？若存在，求出值；若不存在，请说明理由．
如图，请根据图象所提供的信息解答下列问题：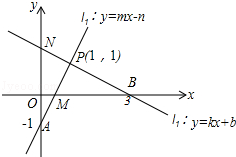
（1）当x 时，kx+b≥mx-n；
（2）不等式kx+b＜0的解集是 ；
（3）交点P的坐标（1，1）是一元二次方程组： 的解；
（4）若直线l1分别交x轴、y轴于点M、A，直线l2分别交x轴、y轴于点B、N，求点M的坐标和四边形OMPN的面积．
如图，▱ABCD中，BD⊥AD，∠A=45°，E、F分别是AB，CD上的点，且BE=DF，连接EF交BD于O．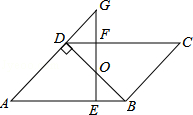
（1）求证：BO=DO；
（2）若EF⊥AB，延长EF交AD的延长线于G，当FG=1时，求AD的长．
如图，已知在▱ABCD中，E、F是对角线BD上的两点，BE=DF，点G、H分别在BA和DC的延长线上，且AG=CH，连接GE、EH、HF、FG．求证：四边形GEHF是平行四边形．
学校计划选购甲、乙两种图书作为“校园读书节”的奖品．已知甲图书的单价是乙图书单价的1.5倍；用600元单独购买甲种图书比单独购买乙种图书要少10本．
（1）甲、乙两种图书的单价分别为多少元？
（2）若学校计划购买这两种图书共40本，且投入的经费不超过1050元，要使购买的甲种图书数量 不少于乙种图书的数量，则共有几种购买方案？
请你说明：当n为自然数时，（n+7）2-（n-5）2能被24整除．