计算:
(1)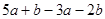
(2)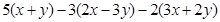
把下列各数填入表示它所在的数集的大括号: 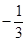 ,
,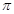 ,
,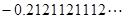 (每两个2之间依次增加1个1),0,
(每两个2之间依次增加1个1),0,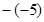 ,
,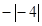 ,
,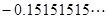
正数集合{ …} 负有理数集合{ …}
整数集合{ …} 无理数集合{ …}
把下列各数:-2.5, , 0,
, 0, ,
,  在数轴上表示出来,并用“<”把它们连接起来.
在数轴上表示出来,并用“<”把它们连接起来.
(12分)出租车司机小李某天上午营运时是在东西走向的大街上进行的,如果规定:向东为正,向西为负,他这天上午所接六位乘客的行车里程(单位:km)如下:-2,+5,-1,+1,-6,-2,问:
(1)将最后一位乘客送到目的地时,小李的位置在.
(2)若汽车耗油量为0.2L/km(升/千米),这天上午小李接送乘客,出租车共耗油多少升?
(3)若出租车起步价为8元,起步里程为2.5km(包括2.5km ),超过部分(不足1千米按1千米计算)每千米1.5元,问小李这天上午共得车费多少元?
(12分)某地电话拨号入网有两种收费方式,用户可以任选其一:
方法一:计时制:0.05元/分;
方法二:包月制:50元/月(限一部个人住宅电话上网).
此外,每一种上网方式都得加收通信费0.02元/分.
(1)设某用户某月上网的时间为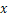 小时,请你分别写出两种收费方式下该用户应该支付的费用;
小时,请你分别写出两种收费方式下该用户应该支付的费用;
(2)若某用户估计一个月内上网的时间为20小时,你认为采用哪种方式较为合算?