请同学们认真阅读、研究，完成“类比猜想”及后面的问题．
习题解答：
习题如图（1），点E、F分别在正方形ABCD的边BC、CD上，∠EAF=45°，连接EF，则EF=BE+DF，说明理由．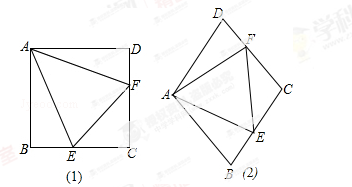

解答：∵正方形ABCD中，AB=AD，∠BAD=∠ADC=∠B=90°，
∴把△ABE绕点A逆时针旋转90°至△ADE′，点F、D、E′在一条直线上．
∴∠E′AF=90°﹣45°=45°=∠EAF，
又∵AE′=AE，AF=AF
∴△AE′F≌△AEF（SAS）
∴EF=E′F=DE′+DF=BE+DF．
习题研究
观察分析：观察图（1），由解答可知，该题有用的条件是①ABCD是四边形，点E、F分别在边BC、CD上；②AB=AD；③∠B=∠D=90°；④∠EAF=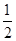∠BAD．
类比猜想：（1）在四边形ABCD中，点E、F分别在BC、CD上，当AB=AD，∠B=∠D时，还有EF=BE+DF吗？
研究一个问题，常从特例入手，请同学们研究：如图13（2），在菱形ABCD中，点E、F分别在BC、CD上，当∠BAD=120°，∠EAF=60°时，还有EF=BE+DF吗？
（2）在四边形ABCD中，点E、F分别在BC、CD上，当AB=AD，∠B+∠D=180°，∠EAF=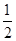∠BAD时，EF=BE+DF吗？
归纳概括：反思前面的解答，思考每个条件的作用，可以得到一个结论“EF=BE+DF”的一般命题：       ．

科目 数学   题型 解答题   难度 较难

知识点： 圆内接四边形的性质