（本题8分）某地为了鼓励居民节约用水，决定实行两级收费制，即每月用水量不超过14吨（含14吨）时，每吨按政府补贴优惠价收费；每月超过14吨时，超过部分每吨按市场调节价收费，小英家1月份用水20吨，交水费29元；2月份用水18吨，交水费24元。
（1）求每吨水的政府补贴优惠价和市场调节价分别是多少？
（2）小英家3月份用水24吨，她家应交水费多少元？
第一次模拟试后，数学科陈老师把一班的数学成绩制成如图的统计图，并给了几个信息：①前两组的频率和是0.14；②第一组的频率是0.02；③自左到右第二、三、四组的频数比为3：9：8，然后布置学生（也请你一起）结合统计图完成下列问题：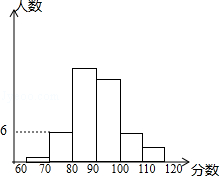
（1）全班学生是多少人？
（2）成绩不少于90分为优秀，那么全班成绩的优秀率是多少？
（3）若不少于100分可以得到A+等级，则小明得到A+的概率是多少？
（1）计算：2014﹣（﹣1）2014+
﹣|﹣3
|
（2）先化简，再求值：
﹣
÷
，其中x=4cos60°+1．
小伟和小欣玩一种抽卡片游戏：将背面完全相同、正面分别写有1，2，3，4的四张卡片背面向上冼匀后，小伟和小欣各自随机抽取一张（不放回）．将小伟的数字作为十位数字，小欣的数字作为个位数字，组成一个两位数．如果所组成的两位数为偶数，则小伟胜；否则小欣胜．
（1）当小伟抽取的卡片数字为2时，问两人谁获胜的可能性大？
（2）通过计算判断这个游戏对小伟和小欣是否公平．
初中生对待学习的态度一直是教育工作者关注的问题之一．为此市教育局对部分学校的八年级学生对待学习的态度进行了一次抽样调查（把学习态度分为三个层级，A级：对学习很感兴趣；B级：对学习较感兴趣；C级：对学习不感兴趣），并将调查结果绘制成图①②的统计图（不完整）．请根据图中提供的信息，解答下列问题：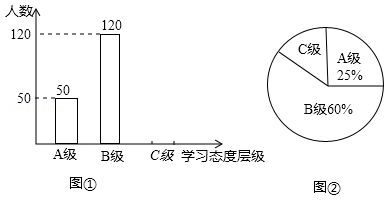
（1）此次抽样调查中，共调查了 名学生；
（2）将图①补充完整；
（3）求出图②中C级所占的圆心角的度数；
（4）根据抽样调查结果，请你估计我市近50000名八年级学生中大约有多少名学生学习态度达标（达标包括A级和B级）？
先化简
，其中x满足x2﹣5x﹣6=0．