初中生对待学习的态度一直是教育工作者关注的问题之一．为此市教育局对部分学校的八年级学生对待学习的态度进行了一次抽样调查（把学习态度分为三个层级，A级：对学习很感兴趣；B级：对学习较感兴趣；C级：对学习不感兴趣），并将调查结果绘制成图①②的统计图（不完整）．请根据图中提供的信息，解答下列问题：
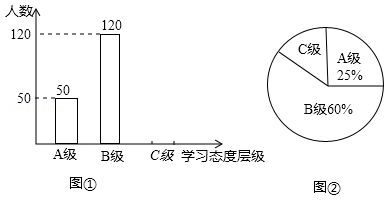
（1）此次抽样调查中，共调查了 名学生；
（2）将图①补充完整；
（3）求出图②中C级所占的圆心角的度数；
（4）根据抽样调查结果，请你估计我市近50000名八年级学生中大约有多少名学生学习态度达标（达标包括A级和B级）？
用适当的方法解下列方程：
（1）
（2）
计算
（1）（
－
）0－
＋
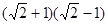（2）
如图，在平面直角坐标系中，点M是第一象限内一点，过M的直线分别交x轴，y轴的正半轴于A，B两点，且M是AB的中点．以OM为直径的⊙P分别交x轴，y轴于C，D两点，交直线AB于点E（位于点M右下方），连结DE交OM于点K．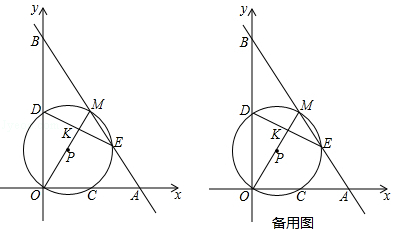
（1）若点M的坐标为（3，4），
①求A，B两点的坐标；
②求ME的长．
（2）若
，求∠OBA的度数．
（3）设tan∠OBA=x（0＜x＜1），
，直接写出y关于x的函数解析式．
请同学们认真阅读下面的一段文字材料，然后解答题目中提出的有关问题．
为解方程
，我们可以将
视为一个整体，然后设
，则原方程可化为
①
解得
，
，当y=1时，
，∴
，
；
当y=4时，
，∴
，
，∴原方程的解为
=
，
=－，
=
，
=－．
解答问题：
（1）填空：在由原方程得到方程①的过程中，利用_________法达到了降次的目的，体现了_________的数学思想．
（2）解方程
．
如图，某船由西向东航行，在点A测得小岛O在北偏东60°，船航行了10海里后到达点B，这时测得小岛O在北偏东45°，船继续航行到点C时，测得小岛O恰好在船的正北方，求此时船到小岛的距离．（结果保留根号）