一艘观光游船从港口A处以北偏东60°的方向出港观光,航行80海里至 C处时发生了侧翻沉船事故,立即发出了求救信号.一艘在港口正东方向B处的海警船接到求救信号,测得事故船在它的北偏东37°方向。
(1)求海警船距离事故船C的距离BC.
(2)若海警船以40海里/小时的速度前往救援,求海警船到达事故船C处大约所需的时间.(温馨提示:sin 53°≈0.8,cos 53°≈0.6)
如图,是由若干个完全相同的小正方体组成的一个几何体.
(1)请画出这个几何体的三视图;
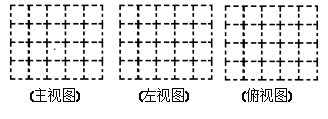
(2)如果在这个几何体上再添加一些相同的小正方体,并保持这个几何体的主视图和俯视图不变,那么最多可以再添加______个小正方体.
邮递员骑车从邮局出发,先向西骑行3km到达A村,继续向西骑行2km到达B村,然后向东骑行7km到达C村,再继续向东骑行3km到达D村,最后骑回邮局.
(1)C村离A村有多远?
(2)邮递员一共骑行了多少千米?
在数轴上把下列各数表示出来,并用“<”连接各数, ,1
,1 ,0,
,0, ,-(+1),4
,-(+1),4
观察下列等式: ,
, ,
, ,
,
将以上三个等式两边分别相加得: .
.
(1)猜想并写出:
(2)直接写出下列各式的计算结果: _____
_____
(3)探究并利用以上规律计算:
历史上的数学巨人欧拉最先把关于 的多项式用记号
的多项式用记号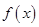 的形式来表示(
的形式来表示(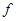 可用其它字母,但不同的字母表示不同的多项式),例如
可用其它字母,但不同的字母表示不同的多项式),例如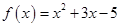 ,把
,把 =某数时的多项式的值用
=某数时的多项式的值用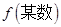 来表示.
来表示.
例如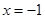 时多项式
时多项式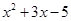 的值记为
的值记为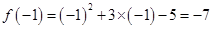 ,
,
已知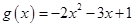 ,
,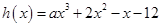
(1)求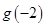 的值
的值
(2)若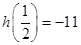 ,求
,求 的值
的值