(本小题满分14分)如图所示,已知圆C与y轴相切于点T(0,2),与x轴正半轴相交于两点M,N(点M在点N的右侧),且|MN|=3,已知椭圆D: +
+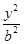 =1(a>b>0)的焦距等于2|ON|,且过点(
=1(a>b>0)的焦距等于2|ON|,且过点(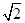 ,
, ).
).
(1)求圆C和椭圆D的方程;
(2)若过点M斜率不为零的直线l与椭圆D交于A、B两点,求证:直线NA与直线NB的倾斜角互补.
若正数项数列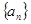 的前
的前 项和为
项和为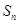 ,首项
,首项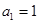 ,点
,点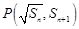 在曲线
在曲线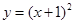 上.
上.
(1)求 ;
;
(2)求数列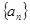 的通项公式
的通项公式 ;
;
(3)设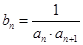 ,
, 表示数列
表示数列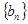 的前项和,若
的前项和,若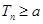 恒成立,求
恒成立,求 及实数
及实数 的取值范围.
的取值范围.
在边长为 的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合,重合后的点记为
的正方形ABCD中,E、F分别为BC、CD的中点,M、N分别为AB、CF的中点,现沿AE、AF、EF折叠,使B、C、D三点重合,重合后的点记为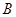 ,构成一个三棱锥.
,构成一个三棱锥.
(1)请判断 与平面
与平面 的位置关系,并给出证明;
的位置关系,并给出证明;
(2)证明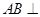 平面
平面 ;
;
(3)求二面角 的余弦值.
的余弦值.
某大学一个专业团队为某专业大学生研究了多款学习软件,其中有A、B、C三种软件投入使用,经一学年使用后,团队调查了这个专业大一四个班的使用情况,从各班抽取的样本人数如下表
| 班级 |
一 |
二 |
三 |
四 |
| 人数 |
3 |
2 |
3 |
4 |
(1)从这12人中随机抽取2人,求这2人恰好来自同一班级的概率.
(2)从这12名学生中,指定甲、乙、丙三人为代表,已知他们下午自习时间每人选择A、B两个软件学习的概率每个都是 ,且他们选择A、B、C任一款软件都是相互独立的.设这三名学生中下午自习时间选软件C的人数为
,且他们选择A、B、C任一款软件都是相互独立的.设这三名学生中下午自习时间选软件C的人数为 ,求
,求 的分布列和数学期望.
的分布列和数学期望.
已知函数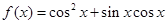 .
.
(1)求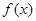 的最小正周期和最小值;
的最小正周期和最小值;
(2)若 且
且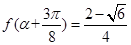 ,求
,求 的值.
的值.
已知函数 .
.
(1)试问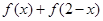 的值是否为定值?若是,求出该定值;若不是,请说明理由;
的值是否为定值?若是,求出该定值;若不是,请说明理由;
(2)定义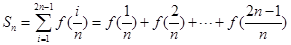 ,其中
,其中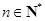 ,求
,求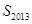 ;
;
(3)在(2)的条件下,令 .若不等式
.若不等式 对
对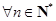 且
且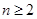 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围.