苏联科学家齐奥尔科夫斯基提出了多级火箭的概念。把火箭一级一级的接在一起，三级火箭从上到下依次为运载物、第三级、第二级和第一级构成，实际应用中一般不会超过四级，可以简化成模型，运载物的质量为M，每一级的质量为m，当运载物和三级物离开地面时已经具有速度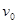
，点火过程连续，上次一点火后紧接着点火下一级（可以看成反冲现象），每一级物分离时速度大小均为
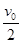，每次分离时间t，M=3m忽略空气阻力，不考虑燃料消耗质量，重力加速度为g。
（1）当第一级与火箭主体分离时，求火箭主体速度
（2）最后一次分离运载物获得推力为多大
如图所示，水平面上固定一轨道，轨道所在平面与水平面垂直，其中bcd是一段以O为圆心、半径为R的圆弧，c为最高点，弯曲段abcde光滑，水平段ef粗糙，两部分平滑连接，a、O与ef在同一水平面上。可视为质点的物块静止于a点，某时刻给物块一个水平向右的初速度，物块沿轨道经过c点时，受到的支持力大小等于其重力的
倍，之后继续沿轨道滑行，最后物块停在轨道的水平部分ef上的某处。已知物块与水平轨道ef的动摩擦因数为μ，重力加速度为g。求：
（1）物块经过c点时速度v的大小；
（2）物块在a点出发时速度v0的大小；
（3）物块在水平部分ef上滑行的距离x。
汽车行驶在半径为50m的圆形水平跑道上，速度为10m/s。已知汽车的质量为1000 kg，汽车与地面的最大静摩擦力为车重的0.8倍。问：（g =10m/s2）
（1）汽车绕跑道一圈需要的时间是多少？角速度是多少？其向心力是多大？（3分×3=9分）
（2）要使汽车不打滑，则其速度最大不能超过多少？
如图所示，将一个小球从h=20m高处水平抛出，小球落到地面的位置与抛出点的水平距离x=30m。取g=10m/s2，不计空气阻力。
求：（1）小球在空中运动的时间；
（2）小球抛出时速度的大小。
一条河宽d=60m，水速v水=3m/s，船在静水中的行驶速度v船=4m/s。。
求：（1）当小船渡河的时间最小时，则小船渡河的位移为多大？
（2）当小船渡河的位移最小时，则小船渡河的时间为多大？
如图所示，半径为R，内径很小的光滑半圆管竖直放置。两个质量均为m的小球a、b以不同的速度进入管内，a通过最高点A时，对管壁上部的压力为3mg，b通过最高点A时，对管壁下部的压力为0.75mg，求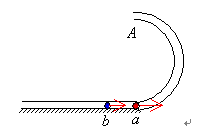
（1）a、b两球在圆管最高点的速度分别是多少？
（2）a、b两球落地点间的距离。