如图所示,一半径为R=0.2m的竖直粗糙圆弧轨道与水平地面相接于B点,C、D两点分别位于轨道的最低点和最高点。距地面高度为h=0.45m的水平台面上有一质量为m=1kg可看作质点的物块,物块在水平向右的恒力F=4N的作用下,由静止开始运动,经过t=2s时间到达平台边缘上的A点,此时撤去恒力F,物块在空中运动至B点时,恰好沿圆弧轨道切线方向滑入轨道,物块运动到圆弧轨道最高点D时对轨道恰好无作用力。物块与平台间的动摩擦因数μ=0.2,空气阻力不计,取g=10m/s2。求
(1)物块到达A点时的速度大小vA。
(2)物块到达B点时的速度大小vB。
(3)物块从B点运动到D点过程中克服摩擦力所做的功。
质量为m=1kg的小物块轻轻放在水平匀速运动的传送带上的P点,随传送带运动到A点后水平抛出,小物块恰好无碰撞的沿圆弧切线从B点进入竖直光滑圆孤轨道下滑。B、C为圆弧的两端点,其连线水平,斜面与圆弧轨道在C点相切连接(小物块经过C点时机械能损失不计)。已知圆弧半径R="1.0" m,圆弧对应圆心角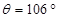 ,轨道最低点为O,A点距水平面的高度h=0.8m。设小物块首次经过C点时为零时刻,在t=0.8s时刻小物块经过D点,小物块与斜面间的滑动摩擦因数为
,轨道最低点为O,A点距水平面的高度h=0.8m。设小物块首次经过C点时为零时刻,在t=0.8s时刻小物块经过D点,小物块与斜面间的滑动摩擦因数为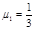 。(g=10m/s2,sin37°=0.6,cos37°=0.8)试求:
。(g=10m/s2,sin37°=0.6,cos37°=0.8)试求:
⑴小物块离开A点的水平初速度vA大小;
⑵小物块经过O点时对轨道的压力;
⑶斜面上CD间的距离。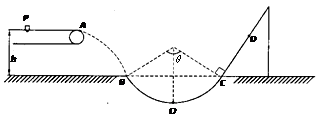
如图所示,在倾角为θ的斜面上静止释放质量均为m的小木箱,相邻两木箱的距离均为L。工人用沿斜面的力推最下面的木箱使之上滑,逐一与其它木箱碰撞(碰撞时间极短)。每次碰撞后木箱都粘在一起运动。整个过程中工人的推力不变,最后恰好能推着三个木箱匀速上滑。已知木箱与斜面间的动摩擦因数为μ,重力加速度为g.,求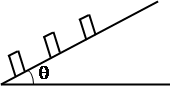
(1)工人的推力;
(2)三个木箱均速运动的速度;
(3)第一次碰撞中损失的机械能。
如图所示,在y轴的右侧存在磁感应强度为B的方向垂直纸面向外的匀强磁场,在x轴的上方有一平行板式加速电场。有一薄绝缘板放置在y轴处,且与纸面垂直。现有一质量为m、电荷量为q的粒子由静止经过加速电压为U的电场加速,然后以垂直于板的方向沿直线从A处穿过绝缘板,而后从x轴上的D处以与x轴负向夹角为30°的方向进入第四象限,若在此时再施加一个电场可以使粒子沿直线到达y轴上的C点(C点在图上未标出)。已知OD长为l,不计粒子的重力.求:
(1)粒子射入绝缘板之前的速度
(2)粒子经过绝缘板时损失了多少动能
(3)所加电场的电场强度和带电粒子在y周的右侧运行的总时间.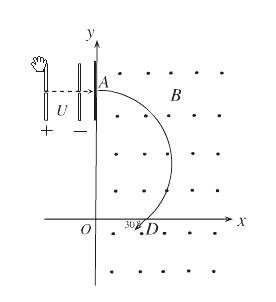
在竖直平面内有一个粗糙的 圆弧轨道,其半径R=0.4m,轨道的最低点距地面高度h=0.45m.一质量m=0.1kg的小滑块从轨道的最高点A由静止释放,到达最低点B时以一定的水平速度离开轨道,落地点C距轨道最低点的水平距离x=0.6m.空气阻力不计,g取10m/s2,求:
圆弧轨道,其半径R=0.4m,轨道的最低点距地面高度h=0.45m.一质量m=0.1kg的小滑块从轨道的最高点A由静止释放,到达最低点B时以一定的水平速度离开轨道,落地点C距轨道最低点的水平距离x=0.6m.空气阻力不计,g取10m/s2,求: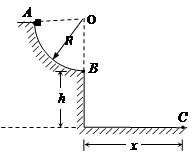
(1)小滑块离开轨道时的速度大小;
(2)小滑块运动到轨道最低点时,对轨道的压力大小;
(3)小滑块在轨道上运动的过程中,克服摩擦力所做的功.
如图所示,光滑绝缘水平面的上方空间被竖直的分界面MN分隔成两部分,左侧空间存在一水平向右的匀强电场,场强大小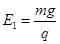 右侧空间有一长为R=0.8m的绝缘轻绳,绳的一端固定于O点,另一端拴一个质量m2=m的不带电的小球B在竖直平面内做顺时针方向的圆周运动,运动到最低点时速度大小vB=8m/s,小球B在最低点时与地面接触但没有弹力. 在MN左侧空间中有一个质量为m1=m的带正电的物体A,电荷量大小为q,在水平面上与MN界面水平间距为L处由静止释放,恰好与运动到最低点处的B发生正碰,并瞬间粘合成一个整体C,碰后瞬间在MN的右侧空间立即加上一竖直向上的匀强电场,场强大小E2=3E1(g=10m/s2)
右侧空间有一长为R=0.8m的绝缘轻绳,绳的一端固定于O点,另一端拴一个质量m2=m的不带电的小球B在竖直平面内做顺时针方向的圆周运动,运动到最低点时速度大小vB=8m/s,小球B在最低点时与地面接触但没有弹力. 在MN左侧空间中有一个质量为m1=m的带正电的物体A,电荷量大小为q,在水平面上与MN界面水平间距为L处由静止释放,恰好与运动到最低点处的B发生正碰,并瞬间粘合成一个整体C,碰后瞬间在MN的右侧空间立即加上一竖直向上的匀强电场,场强大小E2=3E1(g=10m/s2)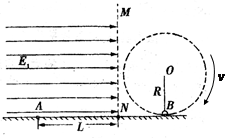
(1)如果L=0.2m,求出整体C运动到最高点时的瞬时速度大小,及此时绳的拉力是物体重力的多少倍?
(2)当L满足什么条件时,整体C可以在竖直面内做一个完整的圆周运动?