（本小题满分12分）为了解甲、乙两厂产品的质量，从两厂生产的产品中分别随机抽取各9件样品，测量产品中某种元素的含量（单位：毫克），如图是测量数据的茎叶图，但是乙厂记录中有一个数字模糊，无法确认，假设这个数字具有随机性，并在图中以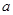
表示，规定：当产品中的此种元素含量不小于18毫克时，该产品为优等品．
（1）若甲、乙两厂产品中该种元素含量的平均值相同，求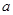的值；
（2）求乙厂该种元素含量的平均值超过甲厂平均值的概率；
（3）当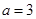
时，利用简单随机抽样的方法,分别在甲、乙两厂该种元素含量超过
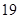（毫克）的数据中个抽取一个做代表,设抽取的两个数据中超过
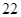（毫克）的个数最多不超过
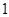个的概率．
已知四棱锥P－ABCD的正视图是一个底边长为4、腰长为3的等腰三角形，如图分别是四棱锥P－ABCD的侧视图和俯视图．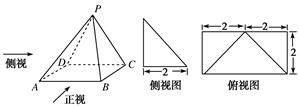
(1)求证：AD⊥PC；
(2)求四棱锥P－ABCD的侧面PAB的面积．
一个几何体的三视图如下图所示，已知正(主)视图是底边长为1的平行四边形，侧(左)视图是一个长为
，宽为1的矩形，俯视图为两个边长为1的正方形拼成的矩形．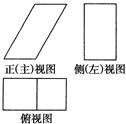
(1)求该几何体的体积V；
(2)求该几何体的表面积S.
如图，点C是以AB为直径的圆上的一点，直角梯形BCDE所在平面与圆O所在平面垂直，且DE∥BC，DC⊥BC，DE＝
BC.
(1)证明：EO∥平面ACD；
(2)证明：平面ACD⊥平面BCDE.
如图，在三棱锥S－ABC中，平面SAB⊥平面SBC，AB⊥BC，AS＝AB.过A作AF⊥SB，垂足为F，点E，G分别是棱SA，SC的中点．
求证：(1)平面EFG∥平面ABC；(2)BC⊥SA.
已知四棱锥P－ABCD中，底面ABCD为正方形，PD⊥平面ABCD，EC∥PD，且PD＝2EC.
(1)求证：BE∥平面PDA；
(2)若N为线段PB的中点，求证：NE⊥平面PDB.