(本小题满分12分)己知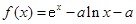 ,其中常数
,其中常数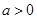 .
.
(1)当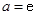 时,求函数
时,求函数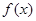 的极值;
的极值;
(2)若函数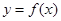 有两个零点
有两个零点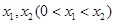 ,求证:
,求证: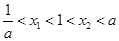 ;
;
(3)求证: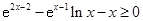 .
.
在四面体ABCD中,AB=AD=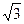 ,BC=CD=3,AC=
,BC=CD=3,AC= ,BD=2.
,BD=2.
(1)平面ABD与平面BCD是否垂直?证明你的结论;(2)求二面角A-CD-B的正切值。
如图,平面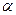 ∥
∥ ,AB和AC是夹在平面
,AB和AC是夹在平面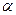 与
与 之间的两条线段,AB⊥AC,且AB=2,直线AB与平面
之间的两条线段,AB⊥AC,且AB=2,直线AB与平面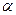 所成角为30°,求线段AC长的取值范围。
所成角为30°,求线段AC长的取值范围。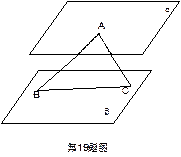
.如图,ABCD-A1B1C1D1是棱长为的正方体,M,N,P,Q,R,S分别是AA1,AB,AD,CC1,B1C1,C1D1的中点,求证:平面PMN∥平面QRS。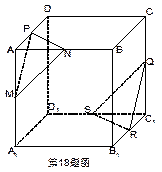
一条隧道的横断面由抛物线弧及一个矩形的三边围成,尺寸如图所示(单位: ),一辆卡车空车时能通过此隧道,现载一集装箱,箱宽3
),一辆卡车空车时能通过此隧道,现载一集装箱,箱宽3 ,车与箱共高
,车与箱共高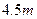 ,此车是否能通过隧道?并说明理由.
,此车是否能通过隧道?并说明理由.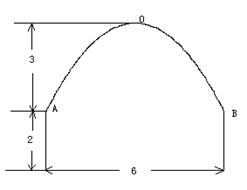
某班40个学生平均分成两组,两组学生某次考试的成绩情况如下表所示:
| 组别 |
平均数 |
标准差 |
| 第一组 |
90 |
4 |
| 第二组 |
80 |
6 |
求这次考试全班的平均成绩和标准差.( 注:平均数 ,
,
标准差 )
)