选修4-1:几何证明选讲
过以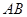 为直径的圆上
为直径的圆上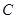 点作直线交圆于
点作直线交圆于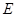 点,交
点,交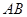 挺长线于
挺长线于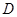 点,过
点,过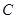 点作圆的切线交
点作圆的切线交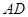 于
于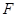 点,交
点,交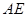 挺长线于
挺长线于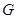 点,且
点,且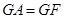 。
。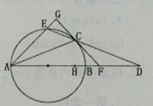
(Ⅰ)求证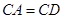 ;
;
(Ⅱ)设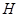 为
为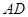 的中点,求证
的中点,求证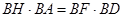
已知函数f(x)=x2+2x+a,x∈[1,+∞).
(1)当a=时,求函数f(x)的最小值;
(2)若对任意x∈[1,+∞),f(x)>0恒成立,试求实数a的取值范围.
设全集U={2,3,a2+2a-3},A={2,|a+1|},∁UA={5}.
(1) 求a的取值集合D;
(2) 若M={x|x=log2|a|,x∈D},求出集合M的所有子集.
求函数的定义域和值域.
| x |
0 |
1 |
2 |
3 |
4 |
5 |
| y |
2 |
3 |
4 |
5 |
6 |
7 |
y=log2(x2-2x+2);
(本小题满分14分)已知数列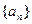 中,
中, ,且
,且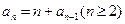 ,求此数列的第
,求此数列的第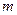 项
项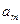 的值
的值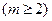 ,现给出此算法流程图的一部分。
,现给出此算法流程图的一部分。
(1)请将空格部分(两个)填上适当内容。
(2)用“For”语句写出相应的算法。
(3)若输出S=16,则输入的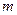 是多少?
是多少?
(本小题满分12分)从含有两件正品 、
、 和一件次品
和一件次品 的3件产品中每次任取一件,连续取两次,求分别在下列两种情况下恰有一件是次品的概率。
的3件产品中每次任取一件,连续取两次,求分别在下列两种情况下恰有一件是次品的概率。
(1)每次取出不放回;
(2)每次取出后放回。