（本小题满分7分）《选修4-4：坐标系与参数方程》
在直角坐标系中，以坐标原点为极点，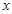
轴的正半轴为极轴建立极坐标系，曲线C的极坐标方程为
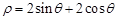，曲线D的参数方程为
（
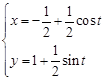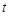为参数）．
（Ⅰ）把C的极坐标方程化为直角坐标方程；
（Ⅱ）判定曲线C与曲线D间的位置关系．
已知点
分别是椭圆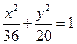
长轴的左、右端点,点
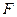是椭圆的右焦点.点
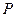在椭圆上,且位于
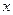轴的上方,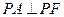
.
（1）求点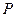的坐标;
（2）设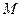
椭圆长轴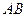
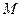上的一点, 到直线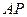
的距离等于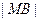
,求椭圆上的点到点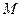的距离
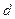的最小值
在数列
中，
，当
时，其前
项和
满足
．
（1）求；
（2）设
，求数列
的前项和
．
（3）求
；
已知函数
满足
且对于任意
, 恒有
成立.
（1）求实数
的值;
（2）解不等式
.
已知向量：a＝(2sinx,2 sinx)，b＝(sinx，
cosx)．
为常数）
（1）若
，求
的最小正周期；
（2）若在[
上最大值与最小值之和为5，求t的值；
（3）在（2）条件下先按
平移后（︱︱最小）再经过伸缩变换后得到
求.
已知方程x2＋y2－2(m＋3)x＋2(1－4m2)y＋16m4＋9＝0表示一个圆．
(1)求实数m的取值范围；(2)求该圆半径r的取值范围；(3)求圆心的轨迹方程．